Month: April 2020

### エンコーダ
複数の入力信号のうち一つが1となった時、これに対応する2進符号を出力する論理回路を指す
e.g. パソコンのキーボード…押しボタンスイッチで文字情報を送付

10進数1桁を2進数4桁(B3,B2,B1,B0)に変換するエンコーダ
2進数4桁で表現された10進数をBCDコード(binary coded decimal code)という

BCDエンコーダの内部回路

BCDデコーダの内部回路

### マルチプレクサ
複数の信号を1つの信号に合成する装置(制御信号がAとBに加え、S=0 or S=1がある)
S=0の時Aを通過させるにはF=!S・Aとし、S=1の時Bを通過させるにはF=S*B

### デマルチプレクサ
1つの信号を複数の信号に分割する、出力選択回路と言われる
A = !S・F, B = S・B(2出力)

### 一致回路
二つのデータが等しいかどうかを判定する回路

### 比較回路
二つのデータの大小を判定する回路を比較回路という

### 加算回路
半加算回路: 1ビット処理
全加算回路: 2ビット以上の場合は下位ビットの桁上げ情報を考慮する
減算は2の補数を用いて加算操作で済ますことができる… 全ビットをNOTゲートで反転させる
ただし、補数を用いた減算で負の結果の場合は、さらに2の補数を求める操作が必要

なるほど、入力値から論理に基づいた出力値になるように、AND,OR,NOR,EXORなどを組み合わせてダイオードの電子回路を引くわけだな。
ロジックだな、電子回路の意味が大分わかってきた。

数理論理学では文字や記号で表現する
A = T -> B = T, A = F -> B = F

論理積OR
0,0 -> 0
0,1 -> 1
1,0 -> 1
1,1 -> 1

論理積AND
0,0 -> 0
0,1 -> 0
1,0 -> 0
1,1 -> 1

論理否定…インバータ
0 -> 1
1 -> 0

[ドモルガンの定理]
ある恒等式が成立していることがわかっていれば、その恒等式に含まれる0を1に、1を0に変換し、論理和を論理積に、論理積を論理和に変換して得られる式も恒等式として成り立つ

### 加法標準法
論理和を結合し、入力状態のうち、いずれか一つが起きた時に、F=1となるよう式を組む
### 乗法標準法
論理積で結合し、入力状態のうち、いずれか一つが起きた時に、F=0となるよう式を組む

### カルノー図
入力変数の値の組み合わせをもとに作成した行と列に出力の値を書き込んだ一覧
論理関数(4入力1出力、3入力2出力)などを簡素化できる

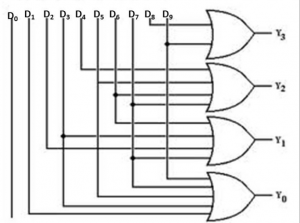
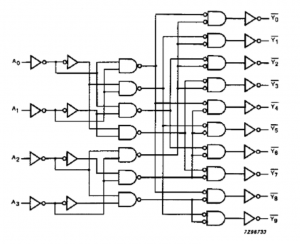
### 論理ゲート
基本回路を論理ゲート(logic gate)といい、通常一つの回路記号で表される
電圧が低い状態(Low)を0に、電圧が高い状態(High)を1に対応させる
どの半導体素子もデジタル回路ではオンとオフを伴ったスイッチの役割を担っている

### ダイオード
P形半導体(電子が不足)からの端子をアノード、N形半導体(余った電子がP原子の周りを回っている)からの端子をカソードといい、アノードからカソードの流れる電流のみを通して、その逆はほとんど通さない
P型は+の電圧、N型は-の電圧
整流作用があり、スイッチと同じ役割を持つ。順バイアスの電圧でオン、逆バイアスの電圧でオフとなり、半導体スイッチという

バイポーラトランジスタも IB>0 or IB = 0でスイッチの役割を果たす(Transistor Transistor Logicで広く使用)
論理回路出力に接続可能な最大ゲート数をファインアウトという

### MOSFET
ゲート、ドレイン、ソース
ゲート、ソース間が絶縁された小容量コンデンサ(直流通過、電荷を蓄える)と等価の構造担っている
一度充電されると、電流はほとんど流れずにオン状態を維持することができる為、電力消費が小さい

### CMOS
二つのMOSFETを直列に接続した構造(complementary MOS)
CMOSでは電源電圧Vccが出力端子から分離される為電流が流れず原理上電力損失は起こらない
CMOS回路では原理上電圧降下が生じない為、より多くのゲートを同時に接続できる

– ORゲート…論理和を実現する論理回路　いずれかがHの場合、ダイオードがオン
– ANDゲート…論理積を実現する回路　両者がHの場合はダイオードがオフ
– NOTゲート…バイポーラトランジスタで実現　AがLのとき、抵抗Rは電流が流れない為F=H　逆にA=Hにすると抵抗Rに電流が流れて電圧が低下する為F=Lとなる

NORゲート(ORとNOTゲートを組み合わせる)　…AND, OR, NOTの基本ゲートを全て表現できる
NANDゲート(ANDとNOTゲートを組み合わせる)　…AND, OR, NOTの基本ゲートを全て表現できる

なるほど、パソコンって、pn接合のダイオードで電圧処理してるのか
こりゃ、エンジニアは電子回路勉強した方が絶対いいな

デジタル回路では0と1の記号だけを使った二進数で数を表す
これはエンジニアであれば誰も知ってることだろう
では、何故2進数を使うのか？

### 二進数を使う理由
スイッチをオフにすると高い電圧が発生、スイッチをオンにすると電圧0
この電圧値に対応するルールを決めると、回路はそのルールを表現する回路になる
デジタル回路は電圧の離散値に意味を持たせ、これを処理する

### 2進数
最上位ビットをMSB、最下位ビットをLSB
デジタル回路では0と1しか表せない為、マイナス符号をそのまま扱うことができない　その為、補数(complement)を使う
※補数とは「元の数」と「補数」を足すと桁上がりが発生しない数のうち、「最大」の数
10進数で「６」の補数は「４」、「１７１」の補数は「８２９」
１１９５＋（１００００－１７１）＝１００００＋１０２４
結果が補数かどうかはオーバフローが発生したかどうかで判断する　オーバーフローが起こらなかった場合は桁数の補数で表す
このようにして減算回路は否定と加算演算で容易に実現ができる
コンピュータでは2進数を4ビットまで対応させた16進数がよく使用される(-8〜7までの数字)
8ビットの場合は２５６(-128〜127) 2^9=512

varchar(255)なども、電圧の離散値で8ビットの256からきていると考えると理解が深まりますな。

アナログとデジタルの違いは
「アナログ」=連続、値と値の間に必ず値が存在する
「デジタル」=離散、値が有限個しか存在しない、値と値の間をジャンプして変化する

### アナログ信号とデジタル信号
アナログ信号は、何らかの影響でノイズが侵入した場合、波形が歪む（オーディオアンプなど）
-> 途中侵入したノイズを受信側で除去することは原理上困難であり、それ故アナログ信号はノイズに弱い
デジタル信号はノイズを除去することが可能であり、ノイズに強い
電圧値がパルス状の波形で値がVHかVLのいずれかの限定された値を入力とし、処理結果をデジタル出力する

デジタル回路とは、アナログ信号(電圧、電気信号)の有限個の値に意味を持たせて処理する回路であり、出力信号も有限個の値にのみ意味を持たせたアナログ波形
アナログ回路とデジタル回路の違いは、信号をアナログ信号と捉えるか、デジタル信号と見るかの違い
デジタル回路では、トランジスタをスイッチとして電圧に何らかの意味を持たせる　トランジススイッチが多いほど複雑な処理が可能になる
Intel4004マイクロプロセッサーは、トランジスターの数がたったの2300個だったが、最新のcpuは10億個ぐらいまで増えている

Corei7 プロセシング・ダイ・トランジスター数382 million
Corei5 プロセシング・ダイ・トランジスター数382 million

電子回路、電磁気、電磁波などの知識が総合的に必要ってことはわかってきたけど、中々理解が深まらん印象だな。プログラミング始めた当初と全く一緒や。近道はないから、入門本をひたすら読み続けるしかなさそうか。

物体が帯びている静電気の量であり、電磁場から受ける作用の大きさを規定する物理量
通常、物体には正と負の電荷(electric charge)が同じ量だけ存在する(中世)
外部に出て行ったり、外部から入ってくると電荷のバランスが崩れ一方の電荷を余分に持つ(帯電)…electrification
ただし、系内の電荷量の総和は常に一定に保たれている
電荷と電荷の間に働く力がクーロン力…同符号同士の場合は反発、異符号同士は引き合う
電荷eの単位はクーロン[C]が用いられる
e= 1.60217733 * 10^-19

### クーロンの法則
二つの点電荷が互いに及ぼし合う力は、両電荷の積に比例し、距離の二乗に反比例する
F[N] = k * q1[C]q2[C] / r^2[m]
比例定数kは真空中で k = 1/4πε0 (真空の誘電率)
複数の電荷が存在(q1,q2,q3..qn)する場合
Σj≠i 1/4πε0 * q1[C]q2[C] / r^2ji * rji / rji

### 電界
静電力が働く空間(電位の傾き)を電界という
電界とは、電荷pは電荷Qからベルトルrにある場合、電界Eから力を受けると考える
電界ベクトルEを連ねてできた曲線を電気力線とよぶ
– 電気力線上の任意の点における接線は電界ベクトルEの方向と一致
– 電気力線は正電荷に始まり、負電荷または無限遠に向かう
– 電気力線は互いに交わらない

導体を電界E0の中に置くと、導体中の電荷は電界によって力を受ける為移動する　導体内の電荷がなくなるまで続き、平衡状態では導体内に電荷は存在しない
与えられた電荷と電位との間には比例関係が成り立つ。この比例係数Cを導体の電気容量(capacitance)という
1組の導体を一般にコンデンサーという

### ガウスの法則
ガウスの法則は電荷と電場との間にどのような関係が成立するのかを教えてくれる法則
ある閉じた曲面を垂直に貫く電気力線の本数はその曲面の内部に存在する電荷の総量Qに比例し,Q/εに等しい

### 電位とは
力学における位置エネルギーの位置に相当する概念、電位から電場を求められる
※電界中にある単位正電荷（+１クーロン）が持っている、位置エネルギー

### 電気容量
電気容量は電荷を加える容器としての導体の電気的性能を表す量で、導体の電位を+1V上昇させるために必要な電荷と定義されている
コンデンサの電荷をたくわえる能力

### 静電エネルギー
電場が持つエネルギー

### 電流
電荷の流れが電流、電流の重要な作用の一つが磁界を作ること

うーん、何だろう、中々ハードルが高い

### オームの法則
– 物質の電流の流しにくさを示す指標が「抵抗率」
– 一般的に動線材料には銅が使われている　銀も抵抗率が低いが高価
– １秒間に1[ C ](クーロン)の電荷が通過したときに1[A](アンペア)流れていると定義される
– 抵抗率と長さは比例、太さは反比例
R[Ω](抵抗値) = ρ[Ωm](抵抗率ロー)　x l[m](長さ)　/ S[m^2](太さ)

### 電源
回路の両端に電位差あるいは電圧を発生する機械によって電子が移動して電流が流れる
電子回路を考える上では「電流」「抵抗」「電圧」を考えなければならない
電子の移動速度I[A]は電圧の大きさE[V]に比例、抵抗の大きさR[Ω]に反比例
I = E/R
P = E * I = I * R * I = I^2R[W]
消費電力とは電気エネルギーのことを指している

### 直接接続と並列接続
直接接続した場合の抵抗はR = R1 + R2と足し算で表す
並列接続した場合は　1/R = 1/R1 + 1/R2 と逆数の足し算で表す

### 直流と交流
直流: 電圧の向きが一定で、電流が一方向に流れる。+と-が明確に決められている。電池やACアダプターなどの出力は直流
交流: 0[V]を中心に時間的に電圧に向きが変化する　1秒間に何回電圧の向きが変化するのかを「周波数」といい、[Hz:ヘルツ]で表す
-> 電圧の向きが交互に交互に変わる

### 抵抗
電気回路、電子回路の一番の基本：種類の選定、抵抗値の大きさ、抵抗の使用電力範囲に注意
炭素皮膜抵抗器(LED)、金属皮膜抵抗器、酸化皮膜抵抗器、巻線抵抗器、セメント抵抗器、チップ抵抗器など用途によって使い分ける
カラーコードが抵抗を表す e.g. 1000+-50[Ω]
許容電力量も重要

### コンデンサ
電子素子、交流電流は通過させるが直流電流は遮る　この性質を利用してノイズ対策などによく使われる
静電容量あるいは容量と呼ばれ、単位は[F:ファラド]
コンデンサは1[μ（マイクロ）]〜1[p(ピコ)F]
アルミ電解コンデンサ[LED]、タンタル電解コンデンサ、セラミックコンデンサ、フィルムコンデンサなどよく使われる
耐電圧が決められている

### スイッチ
電流のON/OFFや回路動作の切り替えに使う
スライドスイッチ、トグルスイッチ: 電源スイッチによく使われる
プッシュスイッチ、ロータリースイッチなど

### トランジスタ・FET
電流量を制御できる素子
三本の足があり、それぞれエミッタ[E]、コレクタ[ C ]、ベース[B]
半導体がpnp構造もしくはnpn構造になっている
FETはゲートに電圧を印加する　ソース、ゲート、ドレイン

### 定電流ダイオード
加える電圧に関わらず一定の電流を流す素子

抵抗やコンデンサ、スイッチ、トランジスタで半導体の電力、電圧を制御してるってことかね？
抵抗やトランジスタの配置は、プログラミングでいうアルゴリズムを考えるようなものかね？
電子回路の構成って、フレームワークみたいにある程度型はあるんでしょうか？それとも、何か作るときは電子回路の設計図をゼロから書くのでしょうか？

文系で独学で電子回路を学んでる人は、どうやって学んでるんやろうか？

### 半導体
導体(電流を流す)と絶縁体(電流を流さない)の中間
不純物を入れることで抵抗率を大きく変えることができる
p型半導体(正の電荷を流す)とn型半導体(負の電荷を流す)を作ることができる
シリコン(Si)やゲルマニウム(Ge)など10^-5 〜　10^10[Ωm]

Siは4価の原子、n型のP(リン)にするには5価、p型のB(ホウ素)にするには3価
Si原子の周りに4つのSi原子がきて電子を1個ずつ共有することで安定した状態を作れる(共有結合)…真性半導体
-> 光や熱など外部からのエネルギーによって物質内を自由に動くことができる自由電子にすることが可能
真性半導体に不純物を添加することで、n型、p型を作ることができ、不純物の量によって抵抗率を変化させることができる

### n型半導体
Si結晶中に最外殻電子数の1つ多い5価のP原子を不純物(ドナー)として添加すると余った電子がP原子の周りを回っている
熱エネルギーなどのわずかなエネルギーで結晶中を自由に移動する自由電子になる
-> 電気的に+隣、+イオンとなる
n型半導体に電圧を加えると+電極の方に電子が移動する

### p型半導体
Si結晶中に最外殻電子数の1つ少ないB原子(ホウ素)を不純物として添加すると、電子が不足した共有結合部分ができる　
欠陥部分に原子が入ってくると電子数が過剰になるので-イオンになる
positive電荷を持った粒子のように振る舞う
n型半導体に電圧を加えると-電極の方に正孔(ホール)が移動する

2種類以上の化合物からなるものは化合物半導体と呼ばれる

### 半導体の用途
センサー、CPU、スマホ、デジカメ、テレビ、洗濯機、冷蔵庫、LEDなど機器制御に多く使われている

### シリコン
半導体に最も多く使われている素材
オーストラリア、ブラジル、中国などから金属シリコンとして輸入している