<script type="text/babel">
(() =>{
function Counter(props){
function countUp(){
alert('count up!');
}
return(
<li style={{backgroundColor:props.color}} onClick={countUp}>
0
</li>
);
}
ReactDOM.render(
<div className="container">
<ul>
<Counter color="red"/>
<Counter color="yellow"/>
<Counter color="blue"/>
</ul>
</div>,
document.getElementById('root')
);
})();
</script>
function Counter(props){
function countUp(color){
alert(color);
}
return(
<li style={{backgroundColor:props.color}} onClick={() =>
countUp(props.color)}>
0
</li>
);
}
<script type="text/babel">
(() =>{
class Counter extends React.Component {
render(){
return(
<li style={{backgroundColor:this.props.color}}>
0
</li>
);
}
}
ReactDOM.render(
<div className="container">
<ul>
<Counter color="red"/>
<Counter color="yellow"/>
<Counter color="blue"/>
</ul>
</div>,
document.getElementById('root')
);
})();
</script>
<script type="text/babel">
(() =>{
class Counter extends React.Component {
constructor(props){
super(props);
this.state = {
count: 10
};
}
render(){
return(
<li style={{backgroundColor:this.props.color}}>
{this.state.count}
</li>
);
}
}
ReactDOM.render(
<div className="container">
<ul>
<Counter color="red"/>
<Counter color="yellow"/>
<Counter color="blue"/>
</ul>
</div>,
document.getElementById('root')
);
})();
</script>
class Counter extends React.Component {
constructor(props){
super(props);
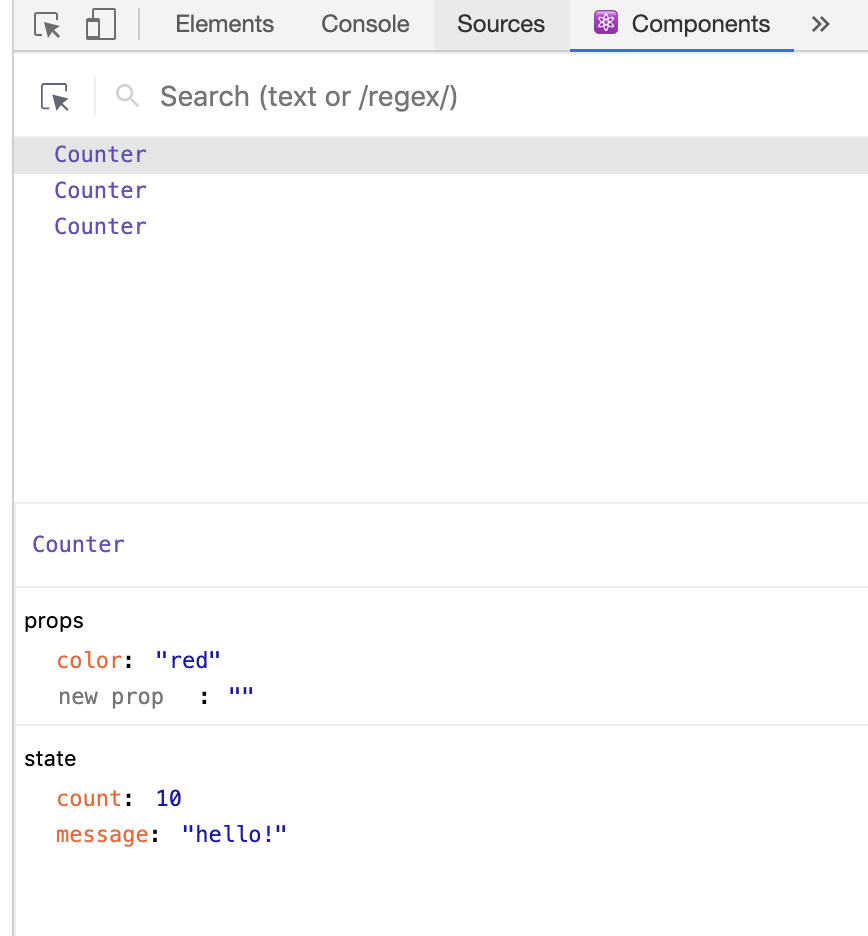
this.state = {
count: 10,
message: 'hello!'
};
}
<script type="text/babel">
(() =>{
class Counter extends React.Component {
constructor(props){
super(props);
this.state = {
count: 0
};
this.countUp = this.countUp.bind(this);
}
countUp(){
this.setState(prevState =>{
return {
count: prevState.count + 1
};
});
}
render(){
return(
<li style={{backgroundColor:this.props.color}} onClick={this.countUp}>
{this.state.count}
</li>
);
}
}
ReactDOM.render(
<div className="container">
<ul>
<Counter color="red"/>
<Counter color="yellow"/>
<Counter color="blue"/>
</ul>
</div>,
document.getElementById('root')
);
})();
</script>
<script type="text/babel">
(() =>{
function Counter(props){
return(
<li style={{backgroundColor:props.counter.color}}>
{props.counter.id}:{props.counter.count}
</li>
);
}
class App extends React.Component {
constructor(){
super();
this.state = {
counters: [
{id: 'A', count: 0, color: 'red'},
{id: 'B', count: 0, color: 'yellow'},
{id: 'C', count: 0, color: 'blue'}
]
};
}
render(){
return (
<div className="container">
<ul>
<Counter counter={this.state.counters[0]}/>
<Counter counter={this.state.counters[1]}/>
<Counter counter={this.state.counters[2]}/>
</ul>
<div>Total Inventory: 3</div>
</div>
)
}
}
ReactDOM.render(
<App/>,
document.getElementById('root')
);
})();
</script>
<script type="text/babel">
(() =>{
function Counter(props){
return(
<li style={{backgroundColor:props.counter.color}}>
{props.counter.id}:{props.counter.count}
</li>
);
}
function CounterList(props){
const counters = props.counters.map(counter => {
return(
<Counter counter={counter}/>
);
});
return (
<ul>
{counters}
</ul>
);
}
class App extends React.Component {
constructor(){
super();
this.state = {
counters: [
{id: 'A', count: 0, color: 'red'},
{id: 'B', count: 0, color: 'yellow'},
{id: 'C', count: 0, color: 'blue'}
]
};
}
render(){
return (
<div className="container">
<CounterList counters={this.state.counters}/>
<div>Total Inventory: 3</div>
</div>
)
}
}
ReactDOM.render(
<App/>,
document.getElementById('root')
);
})();
</script>
function CounterList(props){
const counters = props.counters.map(counter => {
return(
<Counter
counter={counter}
key={counter.id}/>
);
});
<script type="text/babel">
(() =>{
function Counter(props){
return(
<li style={{backgroundColor:props.counter.color}} onClick={() => props.countUp(props.counter)}>
{props.counter.id}:{props.counter.count}
</li>
);
}
function CounterList(props){
const counters = props.counters.map(counter => {
return(
<Counter
counter={counter}
key={counter.id}
countUp={props.countUp}
/>
);
});
return (
<ul>
{counters}
</ul>
);
}
class App extends React.Component {
constructor(){
super();
this.state = {
counters: [
{id: 'A', count: 0, color: 'red'},
{id: 'B', count: 0, color: 'yellow'},
{id: 'C', count: 0, color: 'blue'}
]
};
this.countUp = this.countUp.bind(this);
}
countUp(counter){
this.setState(prevState =>{
const counters = prevState.counters.map(counter => {
return {id: counter.id, count: counter.count, color: counter.color};
});
const pos = counters.map(counter => {
return counter.id;
}). indexOf(counter.id);
counters[pos].count++;
return {
counters: counters
};
});
}
render(){
return (
<div className="container">
<CounterList
counters={this.state.counters}
countUp={this.countUp}
/>
<div>Total Inventory: 3</div>
</div>
)
}
}
ReactDOM.render(
<App/>,
document.getElementById('root')
);
})();
</script>
<script type="text/babel">
(() =>{
function Counter(props){
return(
<li style={{backgroundColor:props.counter.color}} onClick={() => props.countUp(props.counter)}>
{props.counter.id}:{props.counter.count}
</li>
);
}
function CounterList(props){
const counters = props.counters.map(counter => {
return(
<Counter
counter={counter}
key={counter.id}
countUp={props.countUp}
/>
);
});
return (
<ul>
{counters}
</ul>
);
}
class App extends React.Component {
constructor(){
super();
this.state = {
counters: [
{id: 'A', count: 0, color: 'red'},
{id: 'B', count: 0, color: 'yellow'},
{id: 'C', count: 0, color: 'blue'}
],
total: 0
};
this.countUp = this.countUp.bind(this);
}
countUp(counter){
this.setState(prevState =>{
const counters = prevState.counters.map(counter => {
return {id: counter.id, count: counter.count, color: counter.color};
});
const pos = counters.map(counter => {
return counter.id;
}). indexOf(counter.id);
counters[pos].count++;
return {
counters: counters,
total: prevState.total + 1
};
});
}
render(){
return (
<div className="container">
<CounterList
counters={this.state.counters}
countUp={this.countUp}
/>
<div>Total Inventory: {this.state.total}</div>
</div>
)
}
}
ReactDOM.render(
<App/>,
document.getElementById('root')
);
})();
</script>
なるほど、component単位でJavaScriptで作っていくってわけね。少し理解した。