$ npm i -D gulp-eslint
var gulp = require('gulp');
var imagemin = require('gulp-imagemin');
var webserver = require('gulp-webserver');
var sass = require('gulp-sass');
var sassLint = require('gulp-sass-lint');
var eslint = require('gulp-eslint');
var plumber = require('gulp-plumber');
gulp.task('html', function(done){
gulp.src('./src/*.html')
.pipe(gulp.dest('./dest'))
done();
});
gulp.task('js', function(done){
gulp.src(['./src/*.js','!node_modules/**'])
.pipe(eslint({ useEslintrc: true }))
.pipe(eslint.format())
.pipe(eslint.failAfterError())
.pipe(gulp.dest('./dest/js'))
done();
});
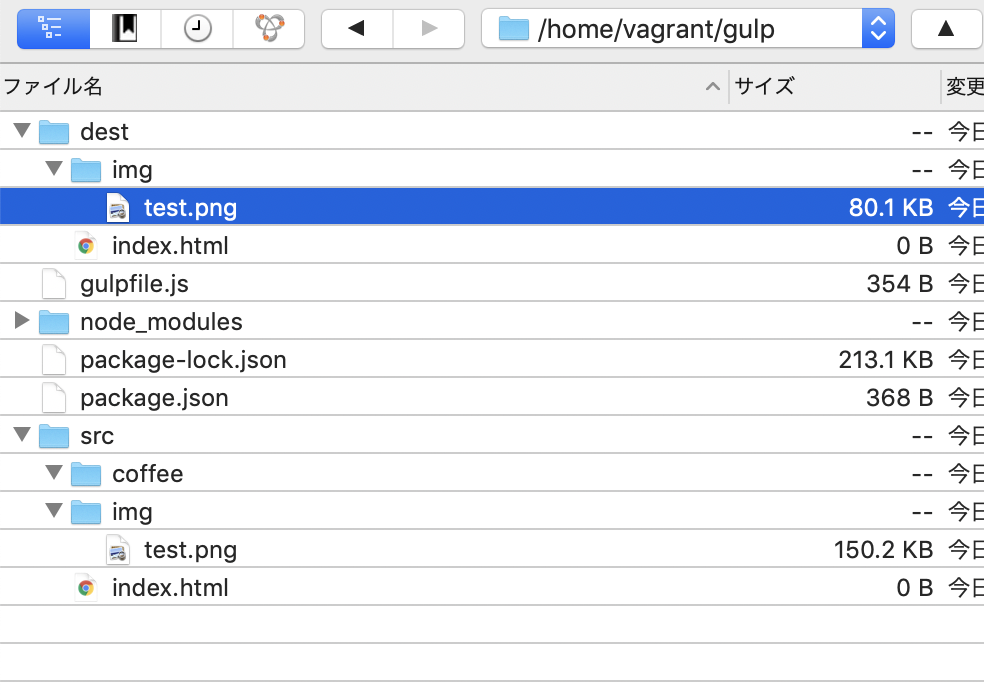
gulp.task('img', function(done){
gulp.src('./src/img/*.png')
.pipe(imagemin())
.pipe(gulp.dest('./dest/img'))
done();
});
gulp.task('sass', function(done){
gulp.src('./src/sass/*.scss')
.pipe(plumber())
.pipe(sassLint())
.pipe(sassLint.format())
.pipe(sassLint.failOnError())
.pipe(sass({outputStyle: 'expand'}))
.pipe(gulp.dest('./dest/css'))
done();
});
gulp.task('watch', function(done){
gulp.watch('./src/*.html', gulp.task('html'))
gulp.watch('./src/js/*.html', gulp.task('js'))
gulp.watch('./src/sass/*.scss', gulp.task('sass'))
done();
});
gulp.task('webserver', function(done){
gulp.src('./dest')
.pipe(webserver({
host:'192.168.34.10',
port: 8000,
livereload: true,
}));
done();
});
gulp.task('default', gulp.series('html','js','img','sass','watch','webserver'));