Category: Math

線形変換とは、ベクトルに行数を掛けてベクトルを作る関数のこと

線形空間を構成するものの基準：標準規定e
標準規定とは、x軸、y軸、z軸の様に座標軸を定めるベクトルの組み

b1 = (3 2) = 3e[x] + 2e[y]

ニューラルネットワークのパラーメータと重みの掛け算は、線形変換

A (a b
c d)

A^-1 = 1/ad – bc(b -d -c a)

行列の内積の計算の際に、右辺や左辺がx,yの時に逆行列を掛けて計算するのかな。
numpy.linalg.inv(X)で算出します。

import numpy as np

a = np.array([[1,2],[4,5]])
print(a)

print(np.linalg.inv(a))

[vagrant@localhost python]$ python app.py
[[1 2]
[4 5]]
[[-1.66666667 0.66666667]
[ 1.33333333 -0.33333333]]
おおおお、なんかすげーな、逆行列も一瞬だな。

で、逆行列だけど、
線形代数使う上では基礎の様。つまり、機械学習に逆行列は必須ってことですね。

行列同士の要素ごとの積を計算する際はnumpy.multiplyを使う
np.multiply(arr1, arr2)
アダマール積と言うらしい。
頭悪い、みたいだな。。

やりたいのは要素同士ではなく、内積の方。
これは何度も出てきている numpy.dot()もしくはnumpy.matmul()を使う

import numpy as np

arr1 = np.arange(1,5).reshape((2,2))
arr2 = np.arange(3,9).reshape((2,3))

print(arr1)
print(arr2)
print(np.dot(arr1,arr2))
print(arr1.dot(arr2))

print(np.matmul(arr1,arr2))

[vagrant@localhost python]$ python app.py
[[1 2]
[3 4]]
[[3 4 5]
[6 7 8]]
[[15 18 21]
[33 40 47]]
[[15 18 21]
[33 40 47]]
[[15 18 21]
[33 40 47]]
おおおおおおおおおおお、素晴らしいですね、これは。
早く画像処理まで行きたいですな。

import numpy as np

arr1 = np.arange(1, 5).reshape((2,2))
arr2 = np.arange(5, 9).reshape((2,2))

print(arr1)
print(arr2)
result = arr1 + arr2
print(result)

print(arr2 - arr1)
print(arr1 * arr2)	
print(arr1 // arr2)	

あれ、掛け算まではわかる。割り算がおかしなことになってる。1/5や1/3は0

cos(a,b) = 内積 / 絶対値|a|*|b| = /|a|*|b|

ベクトル向きが逆の時は -1
直行は　0
平行なら　1

Word2Vecやfasttextなどは、cos類似度で類似テキストを推定していましたね。
例えば、以下の様に、Y1とY2を用意して、X1とどちらが近いかという計算ができます。

import numpy as np

def cos_sim(v1, v2):
	return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))

X1 = np.array([0.782,0.514,0.334,3])
Y1 = np.array([0.457,0.823,0.664,14])
Y2 = np.array([0.256,0.565,0.335,2.4])

print(cos_sim(X1,Y1))
print(cos_sim(X1,Y2))

[vagrant@localhost python]$ python app.py
0.9686648214589598
0.9870228673135825

Cos類似度はY2の方がY1よりも近いと計算できました。

あれ、なんかこれ相関係数に似てるなーと思ったら、、

相関係数とコサイン類似度は数学的にはほぼ等価であり、どちらもベクトルのノルムで正規化した内積です。

やっぱり。。ロジック自体はほぼ一緒でしょうね。

ガウス関数は正規分布関数

a exp{-(x-b)^2 / 2C^2}

こちらもガウス関数の一種
1/√2πσ exp (- (x – μ)^2 / 2σ^2)

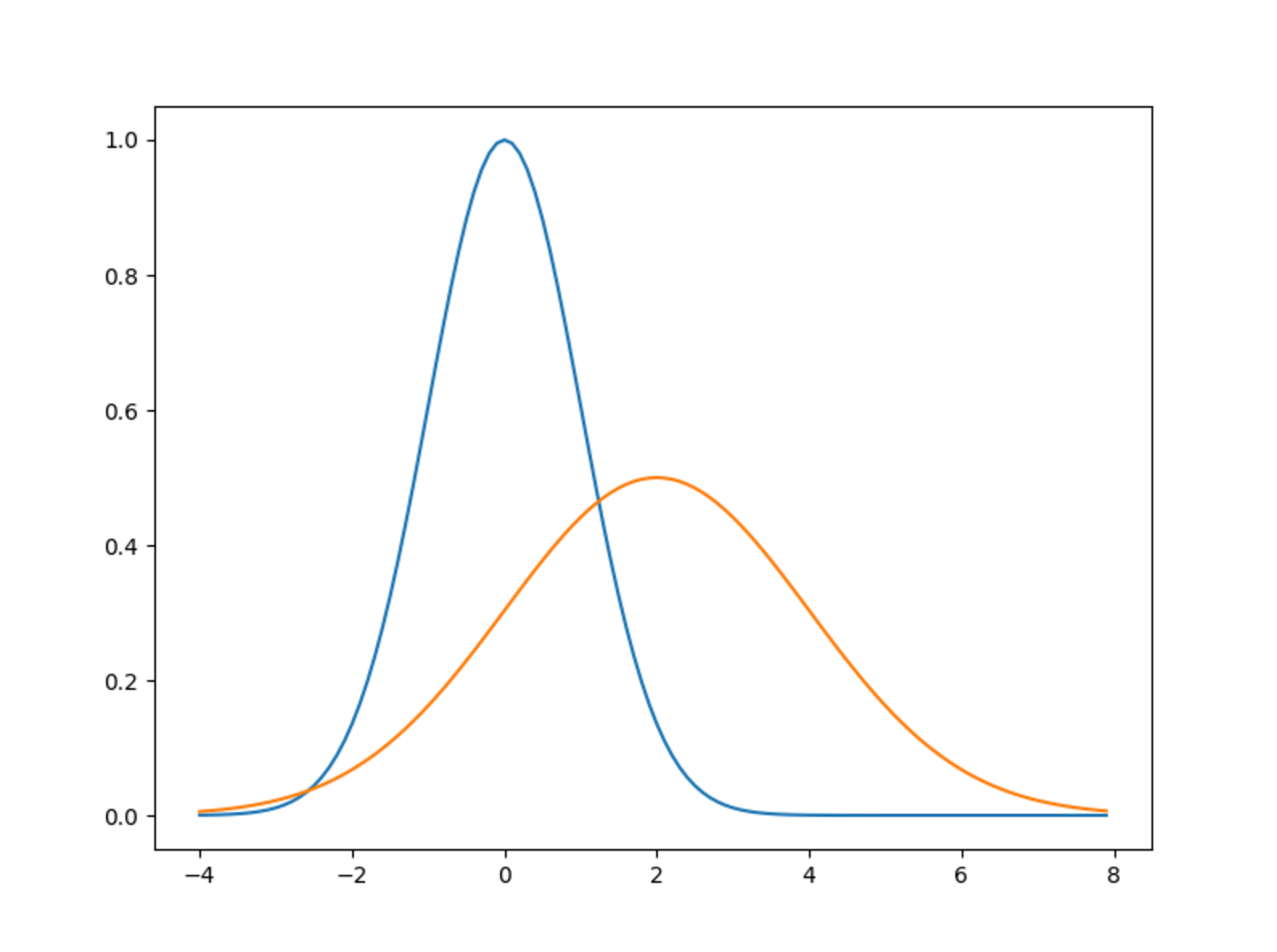
import numpy as np 
import matplotlib.pylab as plt 

def gauss(x, a = 1, mu = 0, sigma = 1):
	return a * np.exp(-(x - mu)**2 / (2*sigma**2))

fig = plt.figure(figsize = (8, 6))
ax = fig.add_subplot(111)

x = np.arange(-4, 8, 0.1)
f1 = gauss(x)
f2 = gauss(x, a = 0.5, mu=2, sigma= 2)

ax.plot(x, f1)
ax.plot(x, f2)

正規分布になってますね。

ガウス分布の微分は
– (x – μ)/√2πσ^3 (- (x – μ)^2 / 2σ^2) です。

一番やりたかったのはこれだが、、

import sympy

x = sympy.Symbol('x')
y = sympy.Symbol('y')

print(sympy.diff(sympy.sin(x)))
print(sympy.diff(sympy.cos(x)))
print(sympy.diff(sympy.tan(x)))

print(sympy.diff(sympy.exp(x)))
print(sympy.diff(sympy.log(x)))

[vagrant@localhost python]$ python app.py
cos(x)
-sin(x)
tan(x)**2 + 1
exp(x)
1/x

あれ、tan(x)の微分は 1/cos^2(x)じゃなかったっけ。。同じって事かな。

math.pi

import math

print(math.pi)

[vagrant@localhost python]$ python app.py
3.141592653589793

角度変換: math.degrees(), math.radians()

import math

print(math.degrees(math.pi))
print(math.radians(180))

[vagrant@localhost python]$ python app.py
180.0
3.141592653589793

import math

print(math.sin(math.radians(30)))
print(round(sin30, 3))
print('{:.3}'.format(sin30))
print(format(sin30,'.3'))

[vagrant@localhost python]$ python app.py
0.49999999999999994
Traceback (most recent call last):
File “app.py”, line 4, in
print(round(sin30, 3))
NameError: name ‘sin30’ is not defined

あれ、sin30って使えない？
あ、sin30 = math.sin(math.radians(30))　で定義してないとダメだね。

import math

cos60 = math.cos(math.radians(60))
print(cos60)

[vagrant@localhost python]$ python app.py
0.5000000000000001

誤差がああああああ

Pythonでは標準モジュールmathを使うと、三角関数(sin,cos,tan)および逆三角関数(arcsin,arccos,arctan)の計算ができる。

は？逆三角関数って何？

通常の三角関数では角度θに応じてyの値を出す
例えば、x = π/3[rad] として、
y = cos π/3 = 1/2

逆関数とは、その逆。値を与えて、角度を得る
あれ、ちょっと待って、sin, cos, tanの y に対する x って1つじゃないよね。。つまり逆三角関数って、螺旋状のようなグラフになるって事かい。。