Category: Math

1でない正数aと正数Nとの間にN = a^bの関係がある時、そのbのこと。
bを、aを底とするNの「対数」と言い、log[a]N = bと表す。
10を底とする常用対数や、eを底とする自然対数を、単に「対数」で指す場合がある

import math
print(math.log10(x) for x in (1,10,100,1000,10000))

ん？

print(math.log10(10))
print(math.log10(-1))

[vagrant@localhost python]$ python app.py
1.0
Traceback (most recent call last):
File “app.py”, line 4, in
print(math.log10(-1))
ValueError: math domain error

import numpy as np 
import matplotlib.pyplot as plt 

x = np.arange(0, 10, 0.01) + 0.00001
y = np.log10(x)
plt.plot(x, y)
plt.savefig('01')

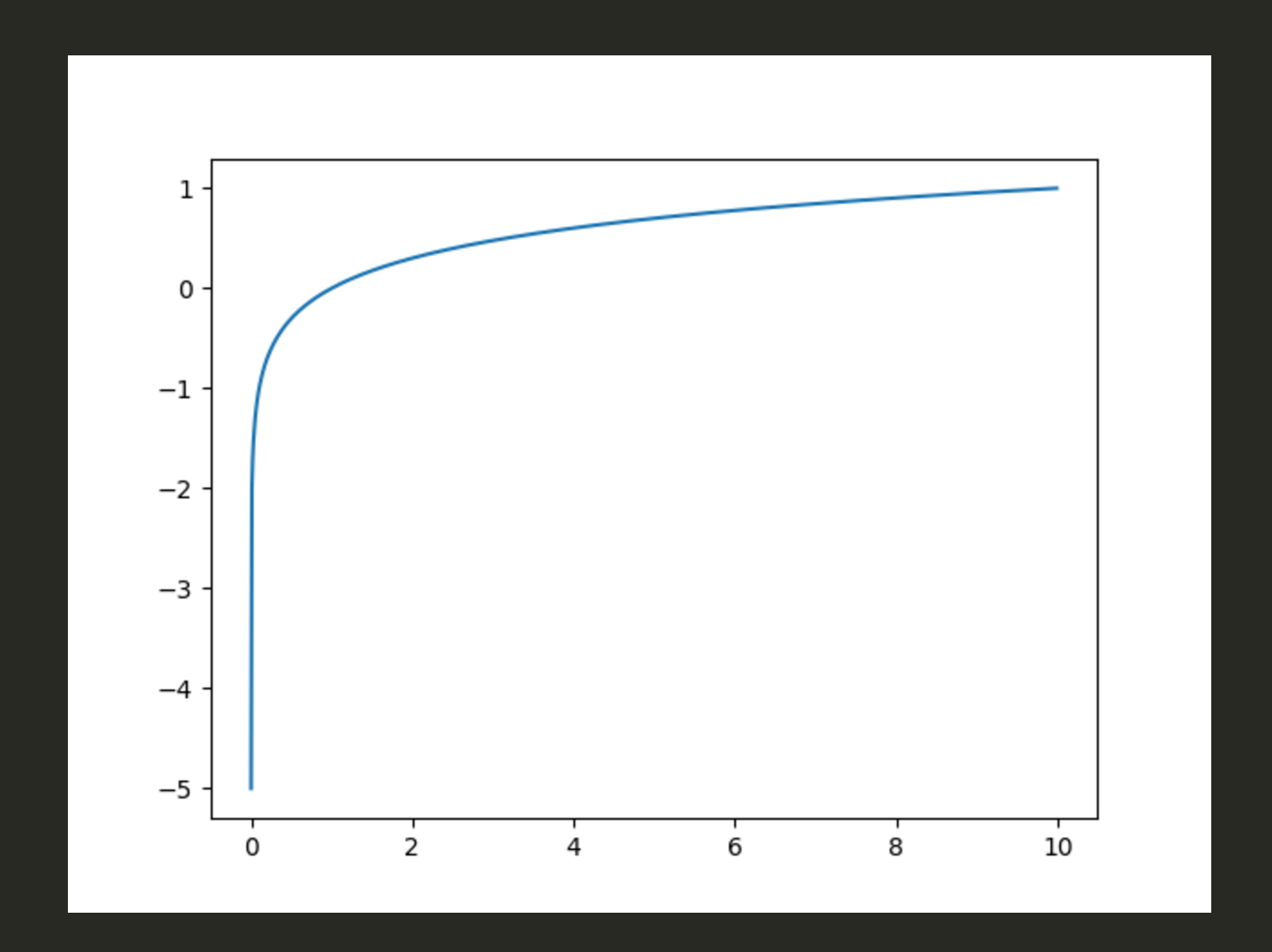
log[10]は0に近づくとマイナスになる。

で、対数って何に使うか？
->　数字がでかくなる時に、y軸を対数スケールにすると分かりやすくなる　…

-> 掛け算、割り算
log[x][y] = log[x] + log[y]
log[x]/[y] = log[x] – log[y]
機械学習には必須。。

-> 2^x = N だから、 x = log[2]N
2分法のアルゴリズムの計算か。あれ、これは結構重要じゃん

「あとどれ位やればある程度マスターできる」って思考が宜しくないね。

mathモジュールを使います

import math

a = math.exp(1)
b = math.exp(2)
c = math.exp(-1)

print("e = {}".format(a))
print("e**2 = {}".format(b))
print("e**(-1) = {}".format(c))

[vagrant@localhost python]$ python app.py
e = 2.718281828459045
e**2 = 7.38905609893065
e**(-1) = 0.36787944117144233

import math

x = math.e

y = len(str(math.e)) - 1

print("e = {}".format(x))
print("桁数 {}".format(y))

[vagrant@localhost python]$ python app.py
e = 2.718281828459045
桁数 16

引き続きmatplotlibを使います。使い方は同じで、三次函数にしただけ。

import matplotlib.pyplot as plt 
import numpy as np 

x = np.arange(-10, 10, 0.1)

y = x**3 - 3*x**2 + 4

plt.plot(x,y)
plt.savefig('01')

グラフを見ると極大、極小を取っていることがわかりますね。
x = 0(極大)
x = 2(極小)

最小2乗法は線形回帰のアルゴリズム。
うむ、なんとも。

matplotlibで書く

import matplotlib.pyplot as plt 
import numpy as np 

x = np.arange(-10, 10, 0.1)

y = x**2 + 10*x + 1

plt.plot(x,y)
plt.savefig('01')

x軸、y軸を定義してplotするだけですね。
感覚的には数式に近いような気がします。

Δy = 0 としてxを変化させると、極限Δx → 0 を考えることができる。これをxについて偏微分したと言う。

from sympy import *
sym.init_printing()

x=Symbol('x')
y=Symbol('y')

print(diff(sin(x),x))
print(diff(exp(x),x))

print(diff(x**4+x**3,x,2))

print(diff(x**2+x*y+2*y**2,x))

print(Derivative(y(t),t))

[vagrant@localhost python]$ python app.py
Traceback (most recent call last):
File “app.py”, line 2, in
sym.init_printing()
NameError: name ‘sym’ is not defined

あれ。。

3x^2 + 5xy + 3y^3
xで偏微分すると　6x + 5y
yで偏微分すると　5y + 9y^2

理屈は簡単ですな。

s1 = {0, 1, 2}
s2 = {1, 2, 3}
s3 = {2, 3, 4}

s_intersection = s1 & s2
print(s_intersection)

s_intersection = s1.intersection(s2)
print(s_intersection)

[vagrant@localhost python]$ python app.py
{1, 2}
{1, 2}

あ、これは面白い

s1 = {0, 1, 2}
s2 = {1, 2, 3}
s3 = {2, 3, 4}

s_difference = s1 - s2
print(s_difference)

s_difference = s2.difference(s1)
print(s_difference)

[vagrant@localhost python]$ python app.py
{0}
{3}

どちらか一方だけに含まれる要素
symmetric_difference

s_symmetric_difference = s1.symmetric_difference(s3)
print(s_symmetric_difference)

[vagrant@localhost python]$ python app.py
{0, 1, 3, 4}
すご。

import numpy as np
rates = np.ones(10) * 3
print(rates ** np.arange(10))

[vagrant@localhost python]$ python myapp.py
[1.0000e+00 3.0000e+00 9.0000e+00 2.7000e+01 8.1000e+01 2.4300e+02
7.2900e+02 2.1870e+03 6.5610e+03 1.9683e+04]

np.ones は配列の全ての要素を1で初期化する