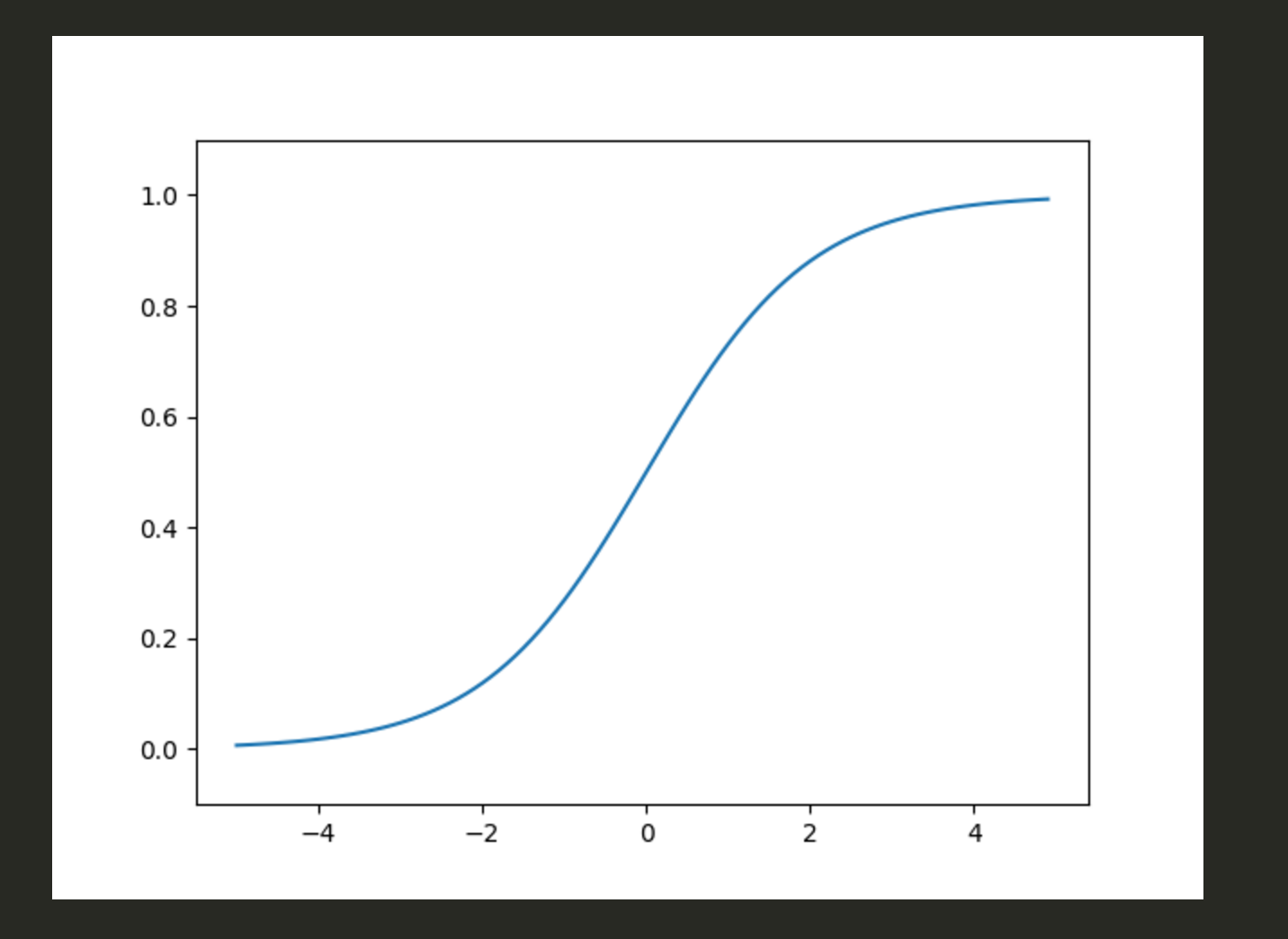
ロジスティック回帰
-> 線形回帰式をシグモイド関数にかけて確率値と解釈
f(x) = 1 / (1 + exp^(-ax)) = a・exp(-ax) / (1 + exp^(-ax))^2
ソフトウェアエンジニアの技術ブログ:Software engineer tech blog
随机应变 ABCD: Always Be Coding and … : хороший
ロジスティック回帰
-> 線形回帰式をシグモイド関数にかけて確率値と解釈
f(x) = 1 / (1 + exp^(-ax)) = a・exp(-ax) / (1 + exp^(-ax))^2

一番やりたかったのはこれだが、、
import sympy
x = sympy.Symbol('x')
y = sympy.Symbol('y')
print(sympy.diff(sympy.sin(x)))
print(sympy.diff(sympy.cos(x)))
print(sympy.diff(sympy.tan(x)))
print(sympy.diff(sympy.exp(x)))
print(sympy.diff(sympy.log(x)))
[vagrant@localhost python]$ python app.py
cos(x)
-sin(x)
tan(x)**2 + 1
exp(x)
1/x
あれ、tan(x)の微分は 1/cos^2(x)じゃなかったっけ。。同じって事かな。
import sympy
x = sympy.Symbol('x')
y = sympy.Symbol('y')
print(type(x))
[vagrant@localhost python]$ python app.py
変数を使っていく
import sympy
x = sympy.Symbol('x')
y = sympy.Symbol('y')
expr = x**2 + y + 1
print(expr)
ほう
[vagrant@localhost python]$ python app.py
x**2 + y
x = sympy.Symbol('x')
y = sympy.Symbol('y')
expr = x**2 + y + 1
print(expr.subs(x,3))
print(expr.subs(x,y))
代入も出来る。完全に再現できるわけね。当たり前か。
[vagrant@localhost python]$ python app.py
y + 10
y**2 + y + 1
xとyの代入も
print(expr.subs([(x,3),(y,2)]))
式の展開
expr = (x + 1)**2 print(sympy.expand(expr))
こいつは凄い
[vagrant@localhost python]$ python app.py
x**2 + 2*x + 1
因数分解
print(sympy.factor(x**3 - x**2 - 3*x + 3)) print(sympy.factor(x*y + x + y + 1))
[vagrant@localhost python]$ python app.py
(x – 1)*(x**2 – 3)
(x + 1)*(y + 1)
何これー
print(sympy.solve(x**2 - 3*x +2)) print(sympy.solve(x**2 + x + 1))
Iは虚数ですね。
[vagrant@localhost python]$ python app.py
[1, 2]
[-1/2 – sqrt(3)*I/2, -1/2 + sqrt(3)*I/2]
で、肝心の微分
来ましたねー
print(sympy.diff(x**3 + 2*x**2 + x)) expr = x**3 + y**2 - y print(sympy.diff(expr, x)) print(sympy.diff(expr, y))
[vagrant@localhost python]$ python app.py
3*x**2 + 4*x + 1
3*x**2
2*y – 1
math.pi
import math print(math.pi)
[vagrant@localhost python]$ python app.py
3.141592653589793
角度変換: math.degrees(), math.radians()
import math print(math.degrees(math.pi)) print(math.radians(180))
[vagrant@localhost python]$ python app.py
180.0
3.141592653589793
import math
print(math.sin(math.radians(30)))
print(round(sin30, 3))
print('{:.3}'.format(sin30))
print(format(sin30,'.3'))
[vagrant@localhost python]$ python app.py
0.49999999999999994
Traceback (most recent call last):
File “app.py”, line 4, in
print(round(sin30, 3))
NameError: name ‘sin30’ is not defined
あれ、sin30って使えない?
あ、sin30 = math.sin(math.radians(30)) で定義してないとダメだね。
import math cos60 = math.cos(math.radians(60)) print(cos60)
[vagrant@localhost python]$ python app.py
0.5000000000000001
誤差がああああああ
Pythonでは標準モジュールmathを使うと、三角関数(sin,cos,tan)および逆三角関数(arcsin,arccos,arctan)の計算ができる。
は?逆三角関数って何?
通常の三角関数では角度θに応じてyの値を出す
例えば、x = π/3[rad] として、
y = cos π/3 = 1/2
逆関数とは、その逆。値を与えて、角度を得る
あれ、ちょっと待って、sin, cos, tanの y に対する x って1つじゃないよね。。つまり逆三角関数って、螺旋状のようなグラフになるって事かい。。
1でない正数aと正数Nとの間にN = a^bの関係がある時、そのbのこと。
bを、aを底とするNの「対数」と言い、log[a]N = bと表す。
10を底とする常用対数や、eを底とする自然対数を、単に「対数」で指す場合がある
import math print(math.log10(x) for x in (1,10,100,1000,10000))
ん?
print(math.log10(10)) print(math.log10(-1))
[vagrant@localhost python]$ python app.py
1.0
Traceback (most recent call last):
File “app.py”, line 4, in
print(math.log10(-1))
ValueError: math domain error
import numpy as np
import matplotlib.pyplot as plt
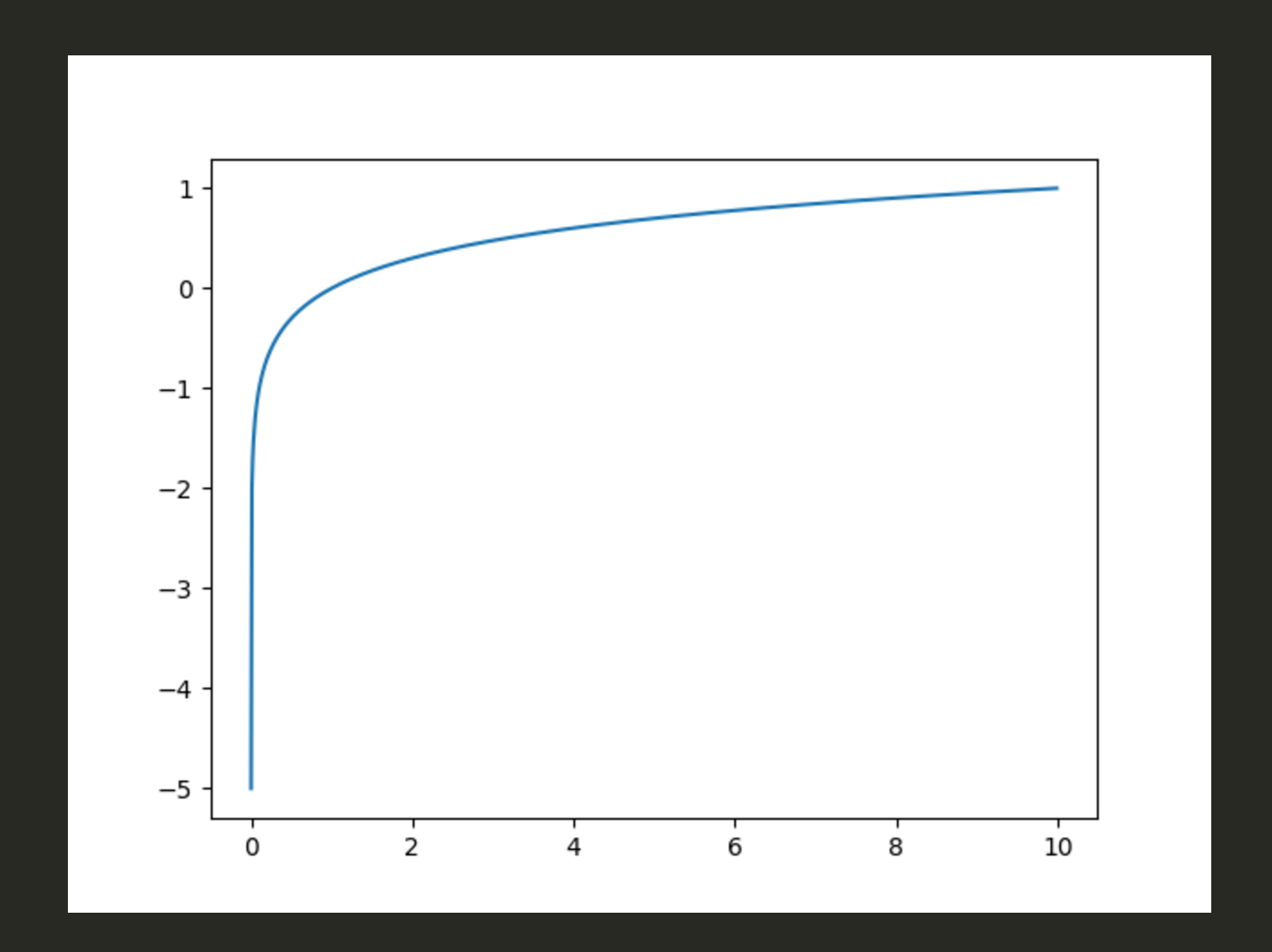
x = np.arange(0, 10, 0.01) + 0.00001
y = np.log10(x)
plt.plot(x, y)
plt.savefig('01')
log[10]は0に近づくとマイナスになる。
で、対数って何に使うか?
-> 数字がでかくなる時に、y軸を対数スケールにすると分かりやすくなる …
-> 掛け算、割り算
log[x][y] = log[x] + log[y]
log[x]/[y] = log[x] – log[y]
機械学習には必須。。
-> 2^x = N だから、 x = log[2]N
2分法のアルゴリズムの計算か。あれ、これは結構重要じゃん
「あとどれ位やればある程度マスターできる」って思考が宜しくないね。
mathモジュールを使います
import math
a = math.exp(1)
b = math.exp(2)
c = math.exp(-1)
print("e = {}".format(a))
print("e**2 = {}".format(b))
print("e**(-1) = {}".format(c))
[vagrant@localhost python]$ python app.py
e = 2.718281828459045
e**2 = 7.38905609893065
e**(-1) = 0.36787944117144233
import math
x = math.e
y = len(str(math.e)) - 1
print("e = {}".format(x))
print("桁数 {}".format(y))
[vagrant@localhost python]$ python app.py
e = 2.718281828459045
桁数 16
引き続きmatplotlibを使います。使い方は同じで、三次函数にしただけ。
import matplotlib.pyplot as plt
import numpy as np
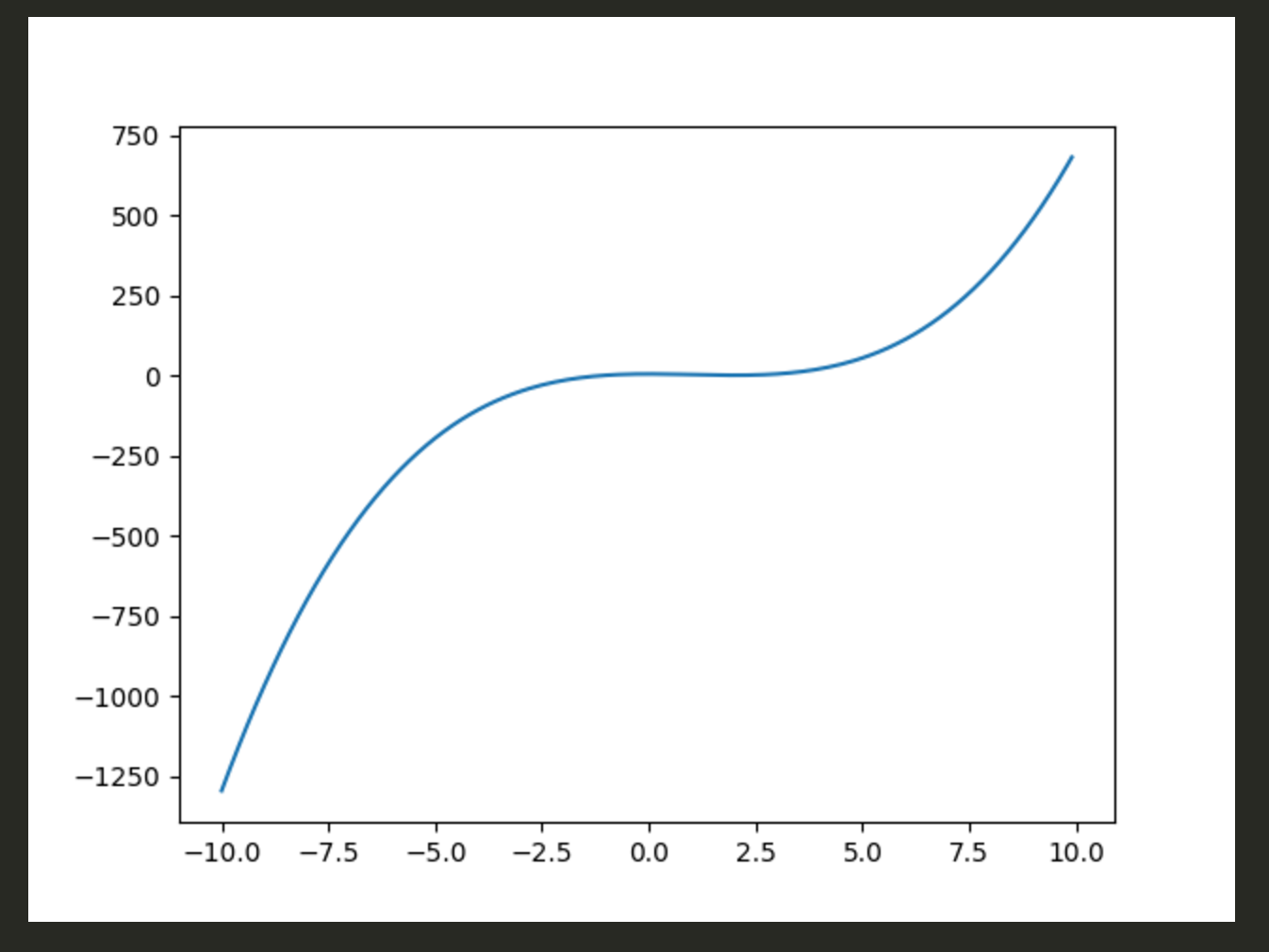
x = np.arange(-10, 10, 0.1)
y = x**3 - 3*x**2 + 4
plt.plot(x,y)
plt.savefig('01')
グラフを見ると極大、極小を取っていることがわかりますね。
x = 0(極大)
x = 2(極小)
最小2乗法は線形回帰のアルゴリズム。
うむ、なんとも。
matplotlibで書く
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-10, 10, 0.1)
y = x**2 + 10*x + 1
plt.plot(x,y)
plt.savefig('01')
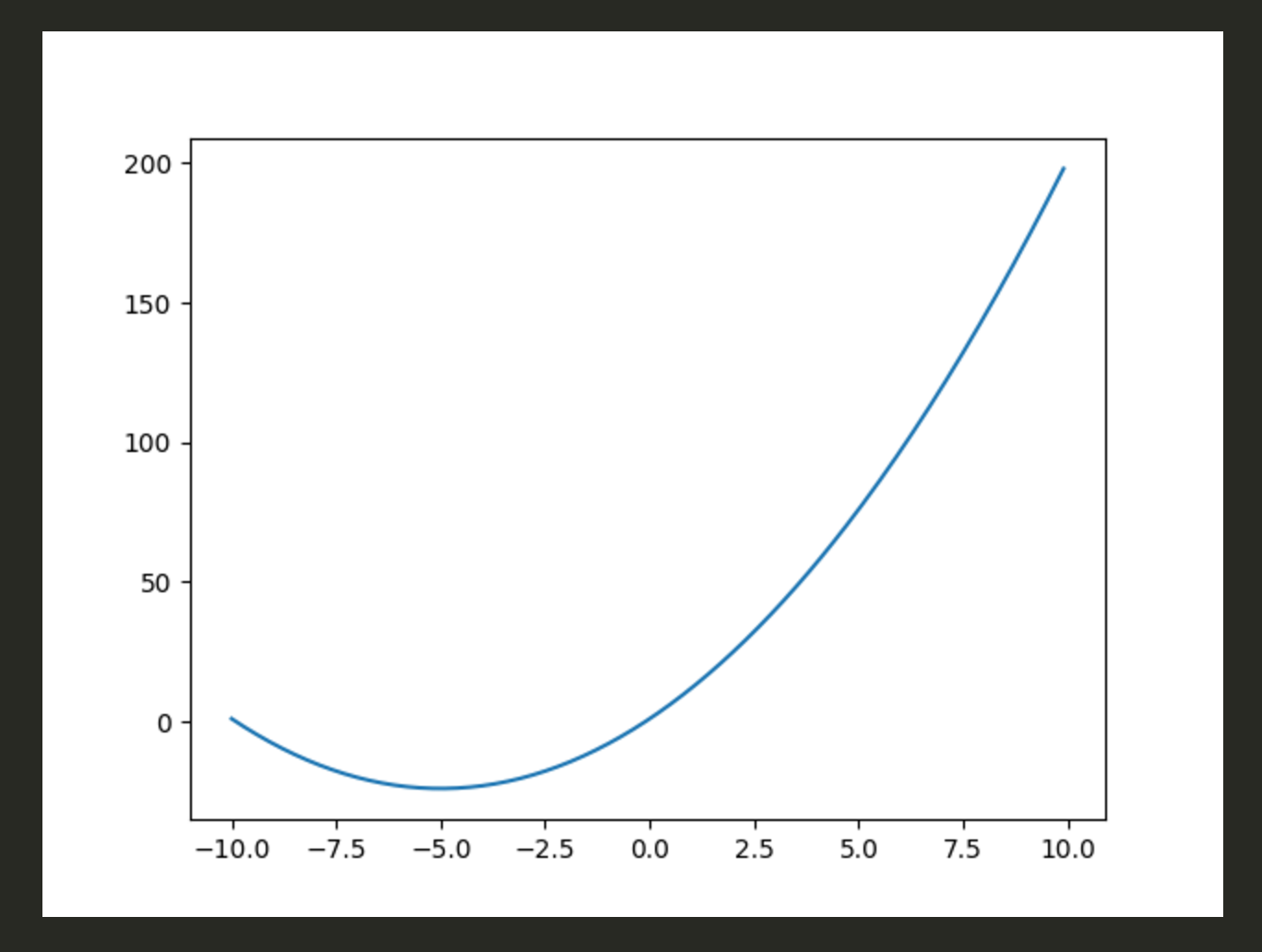
x軸、y軸を定義してplotするだけですね。
感覚的には数式に近いような気がします。
Δy = 0 としてxを変化させると、極限Δx → 0 を考えることができる。これをxについて偏微分したと言う。
from sympy import *
sym.init_printing()
x=Symbol('x')
y=Symbol('y')
print(diff(sin(x),x))
print(diff(exp(x),x))
print(diff(x**4+x**3,x,2))
print(diff(x**2+x*y+2*y**2,x))
print(Derivative(y(t),t))
[vagrant@localhost python]$ python app.py
Traceback (most recent call last):
File “app.py”, line 2, in
sym.init_printing()
NameError: name ‘sym’ is not defined
あれ。。
3x^2 + 5xy + 3y^3
xで偏微分すると 6x + 5y
yで偏微分すると 5y + 9y^2
理屈は簡単ですな。