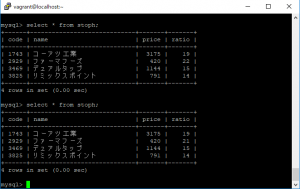
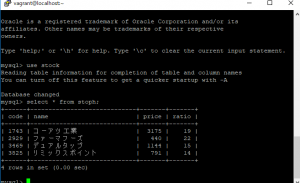
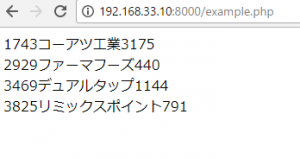
mysql -u root -p で接続します。
[vagrant@localhost api]$ mysql -u root -p
Enter password:
Welcome to the MySQL monitor. Commands end with ; or \g.
Your MySQL connection id is 8
Server version: 5.6.34 MySQL Community Server (GPL)
Copyright (c) 2000, 2016, Oracle and/or its affiliates. All rights reserved.
Oracle is a registered trademark of Oracle Corporation and/or its
affiliates. Other names may be trademarks of their respective
owners.
Type 'help;' or '\h' for help. Type '\c' to clear the current input statement.
次に、データベースをつくります。今回は、”sample”。
mysql> create database sample;
Query OK, 1 row affected (0.11 sec)
テーブルを作成する。
mysql> use sample;
Database changed
mysql> show tables;
Empty set (0.00 sec)
mysql> create table sample.words(
-> id int,
-> word1 varchar(255),
-> word2 varchar(255),
-> word3 varchar(255),
-> word4 varchar(255),
-> word5 varchar(255),
-> word6 varchar(255),
-> word7 varchar(255),
-> word8 varchar(255),
-> word9 varchar(255),
-> word10 varchar(255)
-> );
Query OK, 0 rows affected (0.27 sec)
mysql> show tables;
+------------------+
| Tables_in_sample |
+------------------+
| words |
+------------------+
1 row in set (0.00 sec)
データを挿入します。
mysql> insert into sample.words values
-> (1, 'ワード01','ワード02','ワード03','ワード04','ワード05','ワード06','ワード07','ワード08','ワード09','ワード10'),
-> (2, 'ワード11','ワード12','ワード13','ワード14','ワード15','ワード16','ワード17','ワード18','ワード19','ワード20'),
-> (3, 'ワード21','ワード22','ワード23','ワード24','ワード25','ワード26','ワード27','ワード28','ワード29','ワード30');
Query OK, 3 rows affected (0.07 sec)
Records: 3 Duplicates: 0 Warnings: 0
テーブルのカラムを表示
desc words;
テーブルの中身を表示
select * from words;