ありたいてに言うと、下記のような構造のjsonをfor文で作りたい
{
"item": [
{
"area": "東京都","population": 1300, "capital": "東京"
},
{
"area": "北海道","population": 538, "capital": "札幌市"
},
{
"area": "沖縄","population": 143, "capital": "那覇市"
}
]
}
for文で辞書を配列に入れて、それを辞書の中に入れてjsonにすればOK
ys = cl.OrderedDict()
result = []
for item in data:
print(item["at"][:16] +" " + item["anm"] + " " + item["mag"] + " " + item["maxi"] + " " + item["cod"][:5] + " " + item["cod"][5:11]+ " " + item["cod"][12:-1])
data = cl.OrderedDict()
data["at"] = item["at"][:16]
data["anm"] = item["anm"]
data["mag"] = item["mag"]
data["maxi"] = item["maxi"]
data["tokei"] = item["cod"][:5]
data["hokui"] = item["cod"][5:11]
data["depth"] = item["cod"][12:-1]
result.append(data)
ys["item"] = result
print(ys)
with open("test.json", "w") as f:
json.dump(ys, f, ensure_ascii=False)
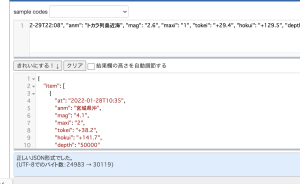
pythonによるjson操作と辞書の理解が浅かったので、これ作るのに丸一日かかった orz…
なんてこったい