Month: September 2019

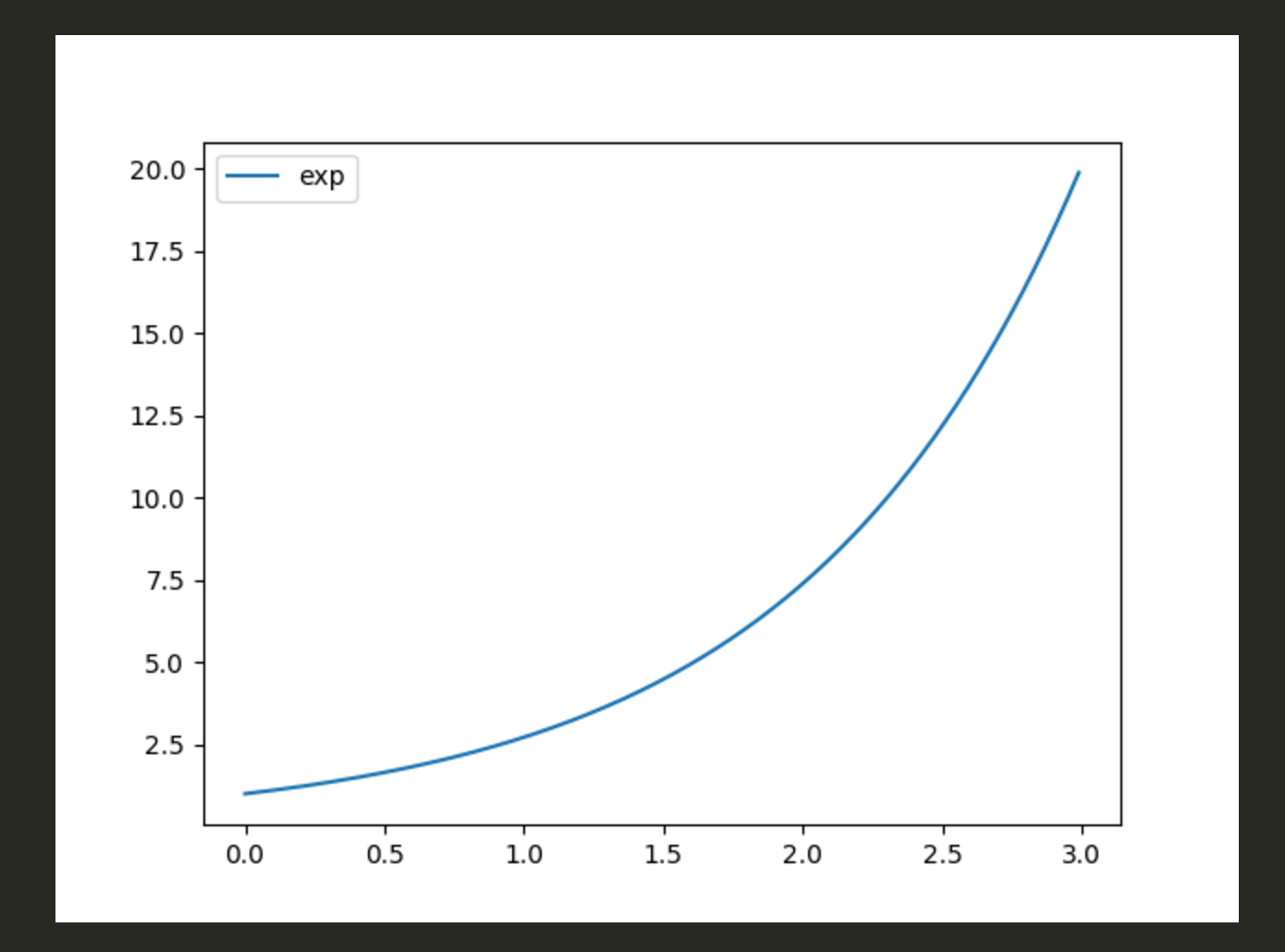
odeintは1階の常微分方程式を解くのに有効な積分器

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt 

def func(y, x, a):
	dydx = a*y
	return dydx

a = 1
y0 = 1
x = np.arange(0, 3, 0.01)

y = odeint(func, y0, x, args=(a,))

plt.plot(x, y, label='exp')
plt.legend()
plt.savefig('01')

import matplotlib.pyplot as plt
import numpy as np 
from scipy.integrate import odeint
from numpy import sin, cos, pi 
from matplotlib.animation import FuncAnimation 

def func(state, t):
	dydt = np.zeros_like(state)
	dydt[0] = state[1]
	dydt[1] = -(G/L)*sin(state[0])
	return dydt 

G = 9.8
L = 1

th1 = 30.0
w1 = 0.0

state = np.radians([th1, w1])

dt = 0.05
t = np.arange(0.0, 20, dt)

sol = odeint(func, state, t)

theta = sol[:, 0]
x = L * sin(theta)
y = - L * cos(theta)

fig = plt.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(-L, L), ylim=(-L, L))
ax.set_aspect('equal')
ax.grid()

line, = ax.plot([], [], 'o-', lw=2)

def animate(i):
	thisx = [0, x[i]]
	thisy = [0, y[i]]

	line.set_date(thisx, thisy)
	return line,

ani = FuncAnimation(fig, animate, frames=np.arange(0, len(t)), interval=25, blit=True)

plt.savefig('01')

極限とは、xの値をある一定値αに限りなく近づけるとき

limit(sin(x)/x, x, 0)
limit(x, x, oo)
limit(1/x,x, oo)
limit(x**x, x, 0)

和集合、積集合、部分集合などの計算の為、pythonのsetを

s = {1, 2, 2, 3, 1, 4}

print(s)
print(type(s))

[vagrant@localhost python]$ python app.py
{1, 2, 3, 4}

s = {i**2 for i in range(5)}

print(s)

s = {1, 2, 2, 3, 1, 4}
print(s)
print(len(s))

[vagrant@localhost python]$ python app.py
{0, 1, 4, 9, 16}
{1, 2, 3, 4}
4

和集合

s1 = {0, 1, 2}
s2 = {1, 2, 3}
s3 = {2, 3, 4}

s_union = s1 | s2
print(s_union)

s_union = s1.union(s2)
print(s_union)

セットで計算

s1 = {0, 1, 2}
s2 = {1, 2, 3}
s3 = {2, 3, 4}

s_union = s1.union(s2,s3)
print(s_union)

等差数列の和の公式は
S = 1/2*n(a + l)
これは基本中の基本でしょう。
pythonで表現します。

範囲の足し算

sum = 0
for i in range(1, 100):
	sum += i
print(sum)

[vagrant@localhost python]$ python myapp.py
4950

forでなく、sumを使う場合

n =99
print(sum(range(1, n + 1)))

[vagrant@localhost python]$ python myapp.py
4950
答えは同じです

公式を使う場合

def sn(a, lim):
	n = int(lim) / a
	l = n * a
	return (a + l) * n / 2
print(sn(3,999))

[vagrant@localhost python]$ python myapp.py
166833.0

公式でもできるが、rangeやsumでできてしまうって事ね。
ただ、これ、気象計算や原子力など計算量が大きくなった場合に何が一番早いかってところだな。