常微分

odeintは1階の常微分方程式を解くのに有効な積分器

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt 

def func(y, x, a):
	dydx = a*y
	return dydx

a = 1
y0 = 1
x = np.arange(0, 3, 0.01)

y = odeint(func, y0, x, args=(a,))

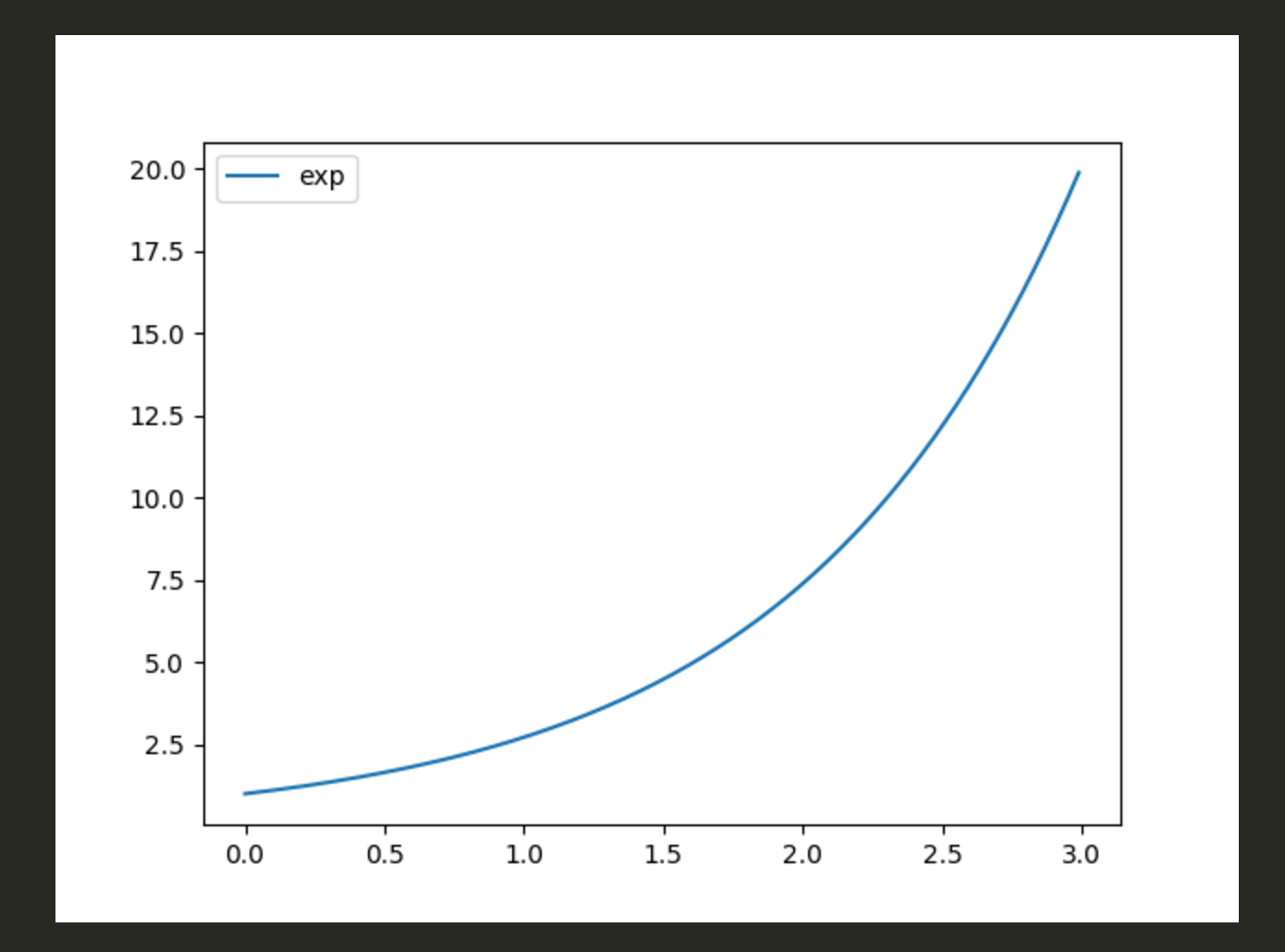
plt.plot(x, y, label='exp')
plt.legend()
plt.savefig('01')

import matplotlib.pyplot as plt
import numpy as np 
from scipy.integrate import odeint
from numpy import sin, cos, pi 
from matplotlib.animation import FuncAnimation 

def func(state, t):
	dydt = np.zeros_like(state)
	dydt[0] = state[1]
	dydt[1] = -(G/L)*sin(state[0])
	return dydt 

G = 9.8
L = 1

th1 = 30.0
w1 = 0.0

state = np.radians([th1, w1])

dt = 0.05
t = np.arange(0.0, 20, dt)

sol = odeint(func, state, t)

theta = sol[:, 0]
x = L * sin(theta)
y = - L * cos(theta)

fig = plt.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(-L, L), ylim=(-L, L))
ax.set_aspect('equal')
ax.grid()

line, = ax.plot([], [], 'o-', lw=2)

def animate(i):
	thisx = [0, x[i]]
	thisy = [0, y[i]]

	line.set_date(thisx, thisy)
	return line,

ani = FuncAnimation(fig, animate, frames=np.arange(0, len(t)), interval=25, blit=True)

plt.savefig('01')