期待値 E(X) は、
E(X) = Σ P(X)X
a = [(-3, 0.977),(24, 0.008), (60, 0.008), (71, 0.006), (99, 0.001)] print(sum(x * p for x, p in a))
[vagrant@localhost python]$ python app.py
-1.734
そういえば、株やFXの自動売買って、期待値を出して瞬時に注文出してるんでしたっけ？？
Month: October 2019
結合確率
複数の事象が同時に起きる確率
simultaneous probability もしくは joint probability という。
P(X, Y)と表記
P(A∩B) = P(A,B) = P(A)P(B)
事象Bが起きた時に事象Aが発生する条件付き確率は
P(A|B) = P(A∩B)/P(B)
機械学習モデルの正確性を表現するには、適合率(Precision), 再現率(Recall)、F値などの指標が使われる
scikit learn
Model evaluation: quantifying the quality of predictions
混合行列(confusion matrix)とは
クラス分類問題の結果を「実際のクラス」と「予想したクラス」を軸にまとめたもの
– TP(Treu Positive)
– TN(True Negative)
– FP(False Positive)
– FN(False Negative)
陽性(Positive)と陰性(Negative)は自分で決められる
from sklearn.metrics import confusion_matrix y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1] y_pred = [1, 0, 1, 1, 1, 0, 0, 0, 1, 1] cm = confusion_matrix(y_true, y_pred) print(cm)
[vagrant@localhost python]$ python app.py
[[1 4]
[3 2]]
なるほど、陽性、陰性は0,1の二進数で表すのね。
TN, FP, FN, TPはそのまま、flatten()で取り出せば良い。
で、正解率(accuracy)は、全てのサンプルのうち、正解したサンプル
$$
\text{accuracy} = \frac{TP + TN}{TP + TN + FP + FN}
$$
from sklearn.metrics import accuracy_score y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1] y_pred = [1, 0, 1, 1, 1, 0, 0, 0, 1, 1] print(accuracy_score(y_true, y_pred))
[vagrant@localhost python]$ python app.py
0.3
陽性と予想したうち、正解したのを適合率
pricision_scoreで示す
TP / TP+FP
再現率（recall）は実際に陽性のサンプルのうち正解したサンプルの割合
TP / TP+FN
F1値は、適合率と再現率の平均調和
つまり、予想に対して正解が高ければ、F1値は1に近づくし、モデルとして優れているということか。。
ロジスティック分布と正規分布
ロジスティック分布：連続確率分布の一つで、その累積分布関数がロジスティック関数であるもの？
パラメーターmu:平均
sigma:スケールパラメータ
import numpy as np import matplotlib.pyplot as plt sigma = 1.0 mu = 0 x = np.arange(-5., 5., 0.001) y = np.exp(-(x-mu)/sigma) / (sigma*(1+np.exp(-(x-mu)/sigma))**2) plt.plot(x,y)
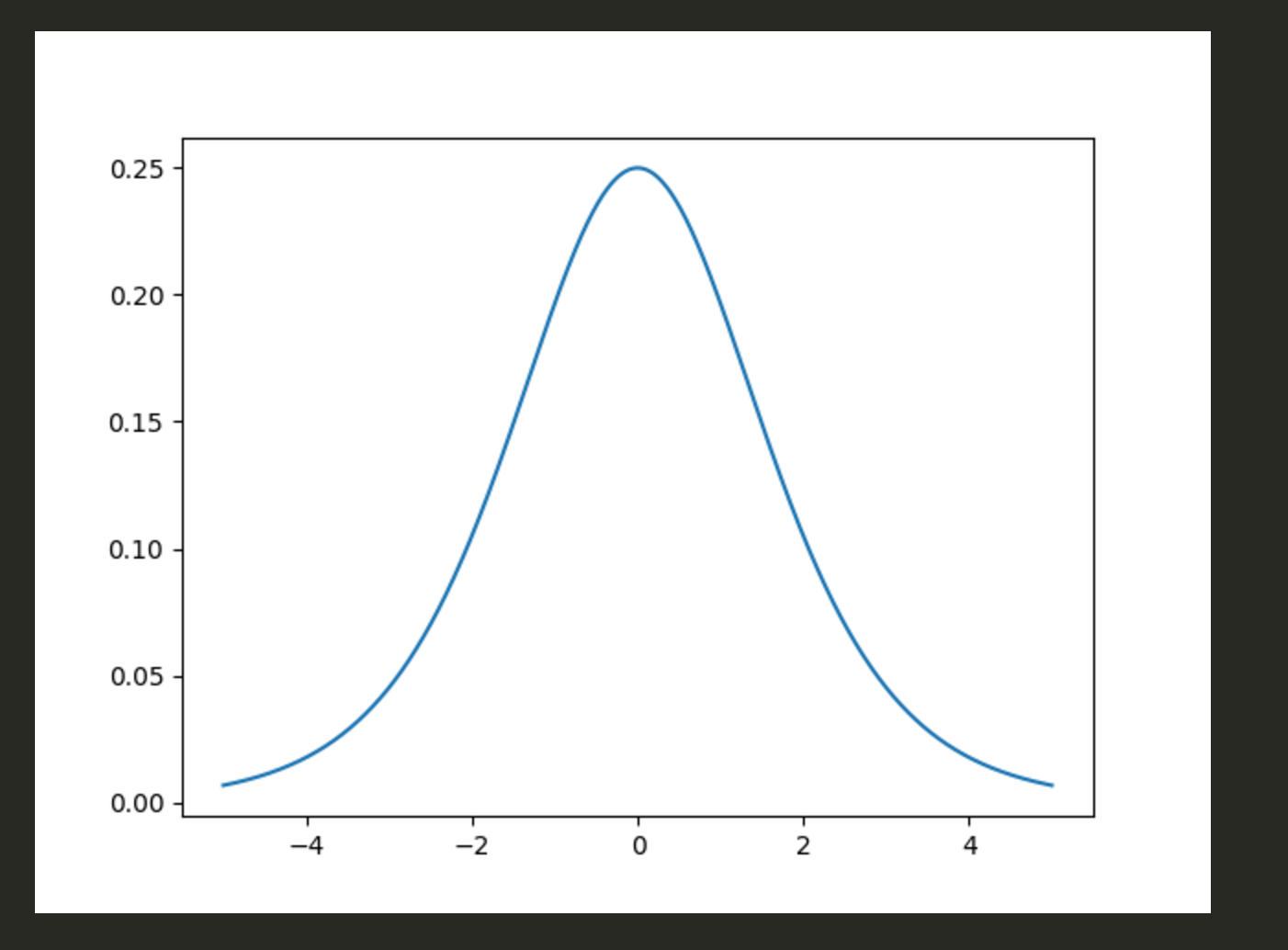
正規分布と見た目は全く一緒だけど、ロジスティック分布は正規分布より裾野が長く、異なるようです。
– 密度関数は平均から離れても下がりにくい
あれ、でも正規分布の特徴である平均値、最頻値、中央値は一致してるのかな。
パレート分布
パレート分布とは所得者の分布？？
import numpy as np import matplotlib.pyplot as plt a, m = 6., 2. s = (np.random.pareto(a, 1000) + 1) * m count, bins, _ = plt.hist(s, 100, density=True) fit = a * m ** a / bins ** (a + 1) plt.plot(bins, max(count) * fit / max(fit), linewidth=2, color='r')
差も然りか。。
指数分布とは？
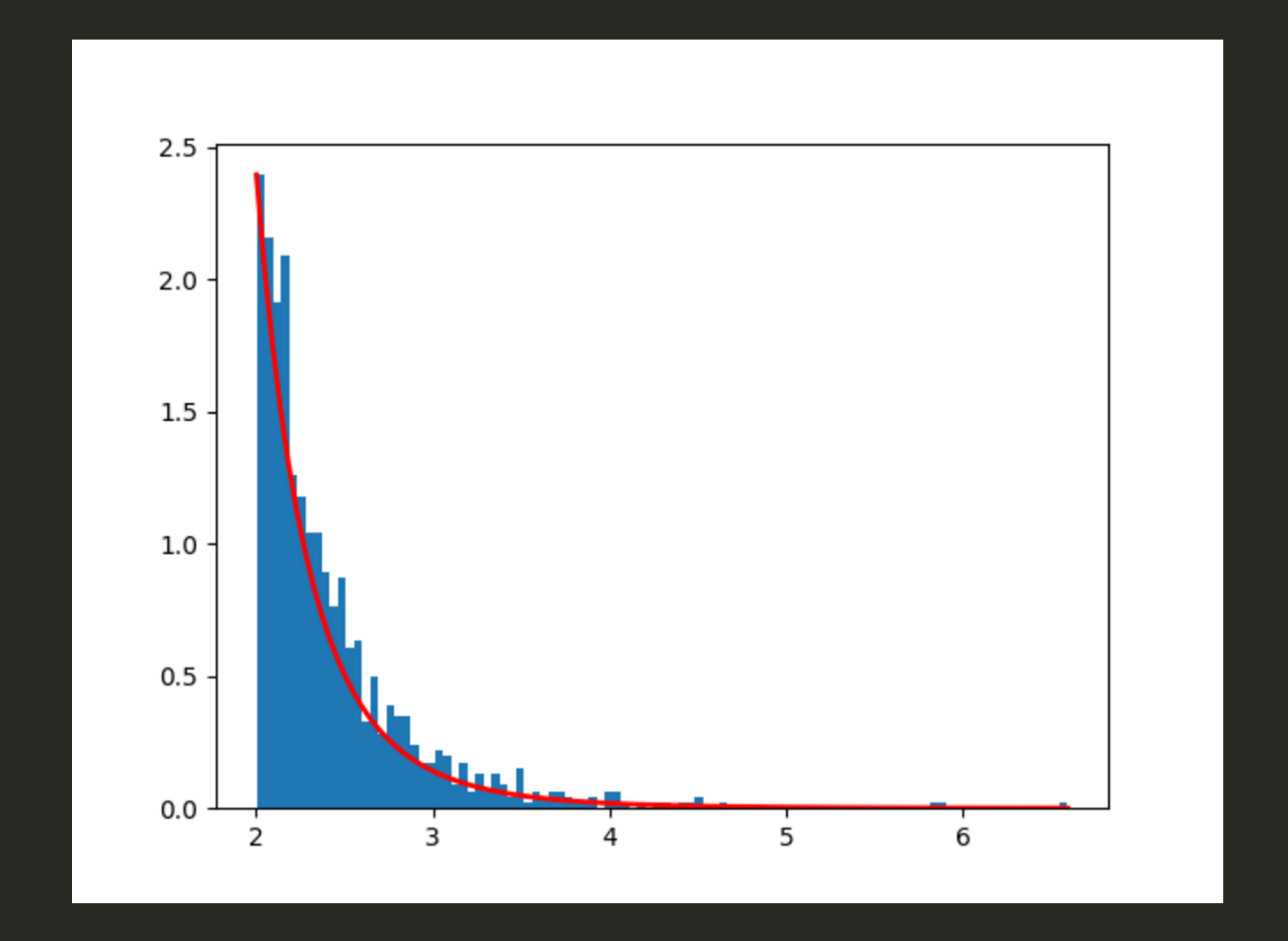
事象が連続して独立に一定の発生率で起こる過程
-> ランダムなイベントの発生間隔を表す分布
e.g. 地震が起きる間隔、電球の寿命
f(x) = 1/μ e ^-x/μ (x>0)
import numpy as np
import math
import matplotlib.pyplot as plt
x = np.arange(-3,3.1,0.1)
y_2 = 2**x
y_3 = 3**x
y_e = math.e**x
y_0_5 = 0.5**x
plt.plot(x,y_2,label="a=2")
plt.plot(x,y_3,label="a=3")
plt.plot(x,y_e,label="a=e")
plt.plot(x,y_0_5,label="a=0.5")
plt.legend()
plt.savefig("01")
正規分布
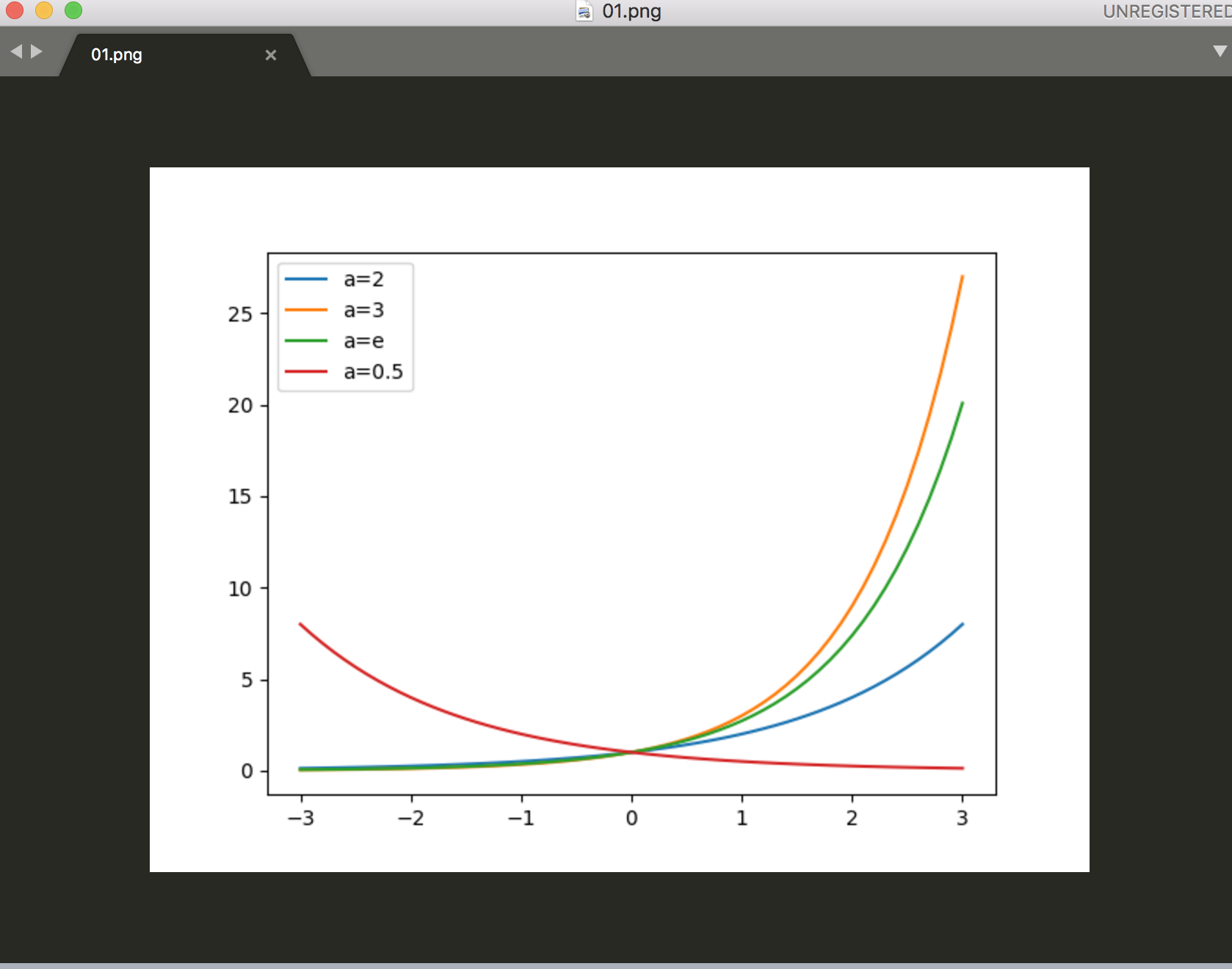
正規分布:平均値の周辺にデータが集積するデータ分布
平均が50、対象が1000、標準偏差が10とする
確率密度を狭めていく
import numpy as np
import matplotlib.pyplot as plt
x = np.random.normal(50, 10, 1000)
plt.hist(x, bins=20)
plt.savefig("01")
plt.hist(x, bins=50)
plt.savefig("02")
plt.hist(x, bins=100)
plt.savefig("03")
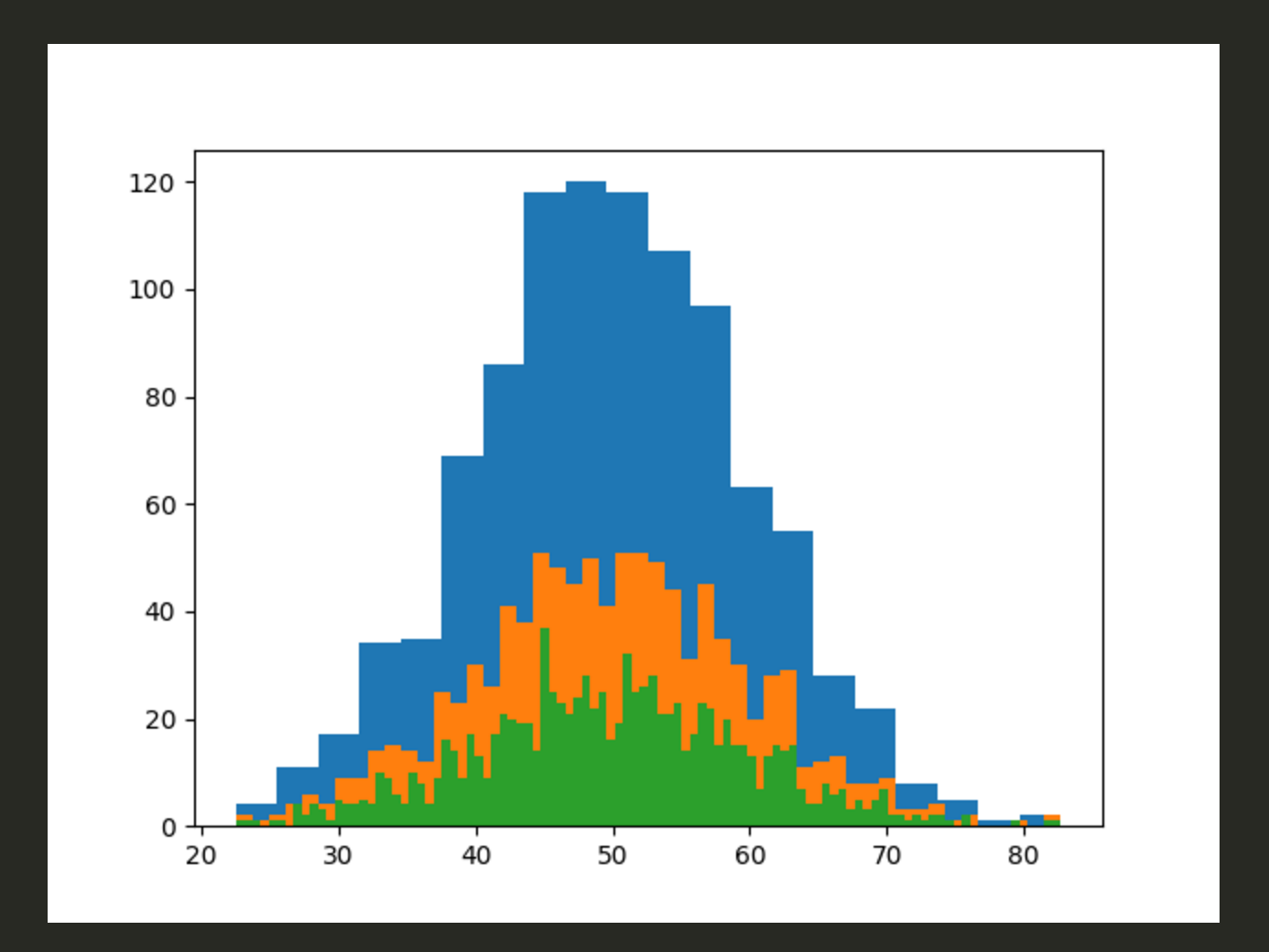
まあ、正常なデータでしょうね。
確率変数
変数Xが確率Pで得られる確率は、P(X)
Xが飛び飛びの場合は、離散型確率変数
続くものは、連続型確率変数(身長、体重、経過時間など)
-> 正規分布、指数分布、スチューデントのt分布、パレート分布、ロジスティック分布などがある。
P(X) = f(x)
ヒストグラムはplt.hist(x)
import numpy as np import matplotlib.pyplot as plt x = np.random.normal(40, 10, 1000) plt.hist(x)
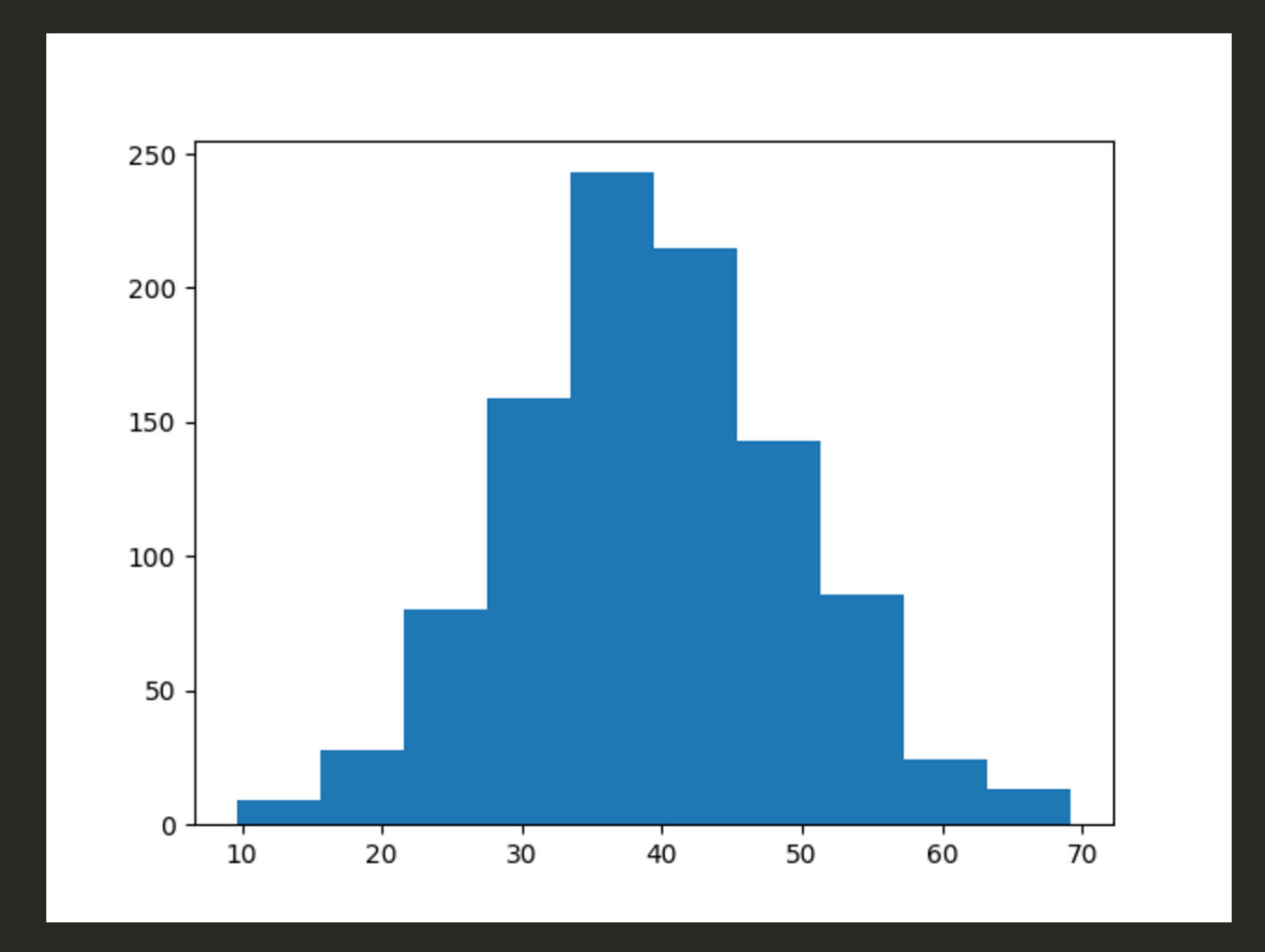
離散確率分布は、ベル・カーブ=正規分布と呼ばれる釣鐘型に近づく。
確率
probabilityを指定する
import numpy as np n = np.random.choice(["a","b","c","d"], p=[0.8, 0.1, 0.05, 0.05]) print(n)
8割の確率で”a”が出力される
[vagrant@localhost python]$ python app.py
a
アルファベットではなく、数字で指定も可能
n = np.random.choice(4, p=[0.8, 0.1, 0.05, 0.05])
import numpy as np n = np.random.choice(4, size=10, p=[0.8, 0.1, 0.05, 0.05]) print(n)
numpyに限らず、ランダム関数は面白いね。
[vagrant@localhost python]$ python app.py
[0 0 0 0 0 0 3 0 0 0]
import numpy as np import pandas as pd import scipy.stats a = pd.Series([5,2,4,9]) print(a.describe())
[vagrant@localhost python]$ python app.py
count 4.00000
mean 5.00000
std 2.94392
min 2.00000
25% 3.50000
50% 4.50000
75% 6.00000
max 9.00000
dtype: float64